题目内容
正三棱锥V-ABC的底面边长为2a，E、F、G、H分别是VA、VB、BC、AC的中点，则四边形EFGH面积的取值范围是（ ）
| A、（0，+∞） | ||||
B、(
| ||||
C、(
| ||||
D、(
|
分析：画出图形，求出EF，HG，说明EFHG是矩形，结合图形，说明V点在ABC平面时，面积最小，求出即可得到范围．
解答：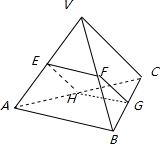
解：由条件可知：EF=HG=a，EFGH是平行四边形
因为正三棱锥V-ABC，所以EFGH是矩形而EH，FG，是变量，
当V点在ABC平面时，VA=VB=VC=
a
此时EH，FG有最小值，EH=FG=
VA=
a
EFGH的面积EF*•EH=a×
a=
a2
故选B．
解：由条件可知：EF=HG=a，EFGH是平行四边形因为正三棱锥V-ABC，所以EFGH是矩形而EH，FG，是变量，
当V点在ABC平面时，VA=VB=VC=
2
| ||
| 3 |
此时EH，FG有最小值，EH=FG=
| 1 |
| 2 |
| ||
| 3 |
EFGH的面积EF*•EH=a×
| ||
| 3 |
| ||
| 3 |
故选B．
点评：本题考查棱锥的结构特征，考查学生作图能力，分析问题解决问题的能力，是基础题．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
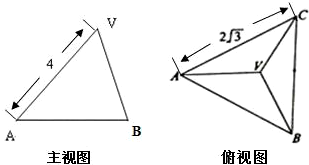已知正三棱锥V-ABC的主视图，俯视图如图所示，其中VA=4，AC=2| 3 |
| A、9 | ||
| B、6 | ||
C、3
| ||
D、
|
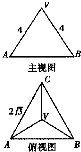如图是正三棱锥V-ABC的主视图，俯视图，根据图中尺寸，则该三棱锥的侧视图面积为（ ）| A、9 | ||||
| B、6 | ||||
C、
| ||||
D、
|
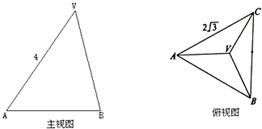（2010•汕头模拟）已知正三棱锥V-ABC的主视图、俯视图如下图所示，其中