题目内容

函数y=sin2x+2cosx(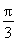≤x≤)的最大值与最小值分别为(　　)

(A)最大值为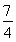,最小值为-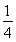

(B)最大值为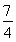,最小值为-2

(C)最大值为2,最小值为-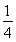

(D)最大值为2,最小值为-2

 

【答案】

B

【解析】化简函数y=sin2x+2cos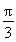x(≤x≤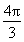)得y=-cos2x+2cosx+1=-(cosx-1)2+2,

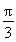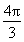当≤x≤时,

cosx∈[-1,],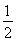

故函数的最小值在cosx=-1时取得为-2,

最大值在cosx=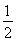时取得为.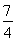

故选B.

 

练习册系列答案
相关题目
设定义在区间(0，
π
2
)上的函数y=sin2x的图象与y=
1
2
cosx图象的交点横坐标为α，则tanα的值为
15
15
15
15
．
给出下列四个命题，其中正确命题的序号是
 

①函数y=sin(2x+
π
6
)的图象可由函数y=sin2x的图象向左平移
π
6
单位得到；
②△ABC中，a，b，c分别是角A，B，C的对边，已知A=60°，a=7，则b+c不可能等于15；
③若函数f（x）的导数为f'（x），f（x0）为f（x）的极值的充要条件是f'（x0）=0；
④在同一坐标系中，函数y=sinx的图象和函数y=x的图象只有一个公共点．
给出下列命题：
①函数y=sin（
2
3
x+
7π
2
）是偶函数；
②函数y=2|x|的最小值是1；
③函数y=ln（x2+1）的值域是R；
④函数y=sin2x的图象向左平移
π
4
个单位，得到y=sin（2x+
π
4
）的图象
⑤函数f（x）=2x-x2只有两个零点；
其中正确命题的序号是
①②⑤
①②⑤
．
把函数y=sin2x的图象沿 x轴向左平移
π
6
个单位，纵坐标伸长到原来的2倍（横坐标不变）后得到函数y=f（x）图象，对于函数y=f（x）有以下四个判断：
①该函数的解析式为y=2sin（2x+
π
6
）；  
②该函数图象关于点（
π
3
，0）对称；　
③该函数在[0，
π
6
]上是增函数；
④函数y=f（x）+a在[0，
π
2
]上的最小值为
3
，则a=2
3
．
其中，正确判断的序号是
②④
②④
．
函数y=sin2x的图象在点P(
π
6
，
1
4
)处的切线的斜率是
3
2
3
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网