题目内容
设P是△ABC内任意一点,S△ABC表示△ABC的面积,λ1=
,λ2=
,λ3=
,定义f(P)=(λ1,λ2,λ3),若G是△ABC的重心,f(Q)=(
,
,
),则( )
| S△PBC |
| S△ABc |
| S△PCA |
| S△ABC |
| S△PAB |
| S△ABC |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| A、点Q在△GAB内 |
| B、点Q在△GBC内 |
| C、点Q在△GCA内 |
| D、点Q与点G重合 |
分析:分析知λ的值对应的是P分△ABC所得三个三角形的高与△ABC的高的比值,比值大,说明相应的小三角形的高比较大,f(Q)=(
,
,
)可以得出Q点离线段AB距离近,故其应在△GAB内.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
解答:解:由已知得,f(P)=(λ1,λ2,λ3)中的三个坐标分别为P分△ABC所得三个三角形的高与△ABC的高的比值,
∵f(Q)=(
,
,
)
∴P离线段AB的距离最近,故点Q在△GAB内
由分析知,
应选A.
∵f(Q)=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴P离线段AB的距离最近,故点Q在△GAB内
由分析知,
应选A.
点评:考查对新定义的理解,此类题关键是通过新给出的定义明了定义所告诉的关系与运算,然后用定义所提供的方式来解题,本题是把相应的坐标与小三角形的高与大三角形的比值对应起来,根据坐标即可得出相应的定点到三个边距离的远近.以此来判断相应的点在大三角形中的相应位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 , λ2=
, λ2= ,λ3=
,λ3= ,定义
,定义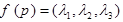 ,若G是△ABC的重心,f(Q)=(
,若G是△ABC的重心,f(Q)=( ,
, ,
, ),则
),则