题目内容
【题目】已知函数f（x）=cos2x，二次函数g（x）满足g（0）=4，且对任意的x∈R，不等式﹣3x2﹣2x+3≤g（x）≤4x+6成立，则函数f（x）+g（x）的最大值为（ ）
A.5
B.6
C.4
D.7
【答案】A
【解析】解：∵二次函数g（x）满足g（0）=4， ∴设g（x）=ax2+bx+4，
由﹣3x2﹣2x+3≤4x+6得3x2+6x+3≥0即3（x+1）2≥0，
即当x=﹣1时，3（x+1）2=0，此时直线y=4x+6与y=﹣3x2﹣2x+3相切，切点为（﹣1，2），
此时g（x）过（﹣1，2），则a﹣2b+4=2，得b= 
+1，
即g（x）=ax2+（ +1）x+4，
由﹣3x2﹣2x+3≤g（x）≤4x+6恒成立得
﹣3x2﹣2x+3≤ax2+（ +1）x+4≤4x+6，
由﹣3x2﹣2x+3≤ax2+（ +1）x+4得（a+3）x2+（ +3）x+1≥0恒成立，当a=﹣3时，不满足条件．
当a≠﹣3时，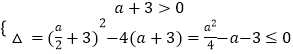 
，得 
得﹣2≤a≤6，
由ax2+（ +1）x+4≤4x+6得ax2+（ ﹣3）﹣2≤0恒成立，当a=0时，不满足条件．
当a≠0时，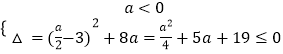 
，得 
，得﹣18≤a≤﹣2，
综上a=﹣2，
则g（x）=﹣2x2+4，当x=0时函数g（x）取得最大值4，
而当x=0时，f（x）=cos2x也取得最大值1，
则函数f（x）+g（x）=cos2x﹣2x2+4的最大值为1+4=5，
故选：A
练习册系列答案
阳光课堂课时作业系列答案
相关题目
