题目内容
在棱长为2的正方体ABCD-A1B1C1D1中，M、N分别是A1B1和B1B的中点．
（1）求直线AM和CN所成角的大小；
（2）若P为B1C1的中点，求证：B1D⊥平面PMN；
（3）求点A到平面PMN的距离．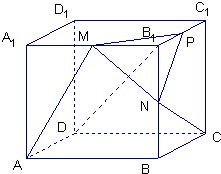
（1）求直线AM和CN所成角的大小；
（2）若P为B1C1的中点，求证：B1D⊥平面PMN；
（3）求点A到平面PMN的距离．
（1）如图，将AM平移到B1E，NC平移到B1F，则∠EB1F为直线AM与CN所成角或其补角
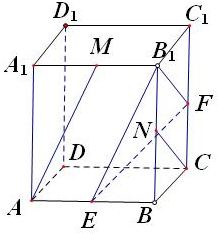
设边长为2，则B1E=B1F=
，EF=
∴由余弦定理得cos∠EB1F=
，
即直线AM和CN所成角的大小为arccos
（2）根据中位线定理可知MN∥A1B，NP∥C1B
∴MN∥平面A1C1B，NP∥平面A1C1B，MN∩NP=P
∴平面A1C1B∥平面MNP，
而B1D⊥平面A1C1B，
所以B1D⊥面PMN；
（3）S△MNP=
，S△MNA=
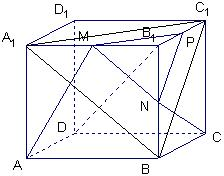
设点A到平面PMN的距离为h
∴VA-MNP=VP-MNA
即
S△MNPh=
S△MNA×1
∴h=
设边长为2，则B1E=B1F=
| 5 |
| 6 |
∴由余弦定理得cos∠EB1F=
| 2 |
| 5 |
即直线AM和CN所成角的大小为arccos
| 2 |
| 5 |
（2）根据中位线定理可知MN∥A1B，NP∥C1B
∴MN∥平面A1C1B，NP∥平面A1C1B，MN∩NP=P
∴平面A1C1B∥平面MNP，
而B1D⊥平面A1C1B，
所以B1D⊥面PMN；
（3）S△MNP=
| ||
| 2 |
| 3 |
| 2 |
设点A到平面PMN的距离为h
∴VA-MNP=VP-MNA
即
| 1 |
| 3 |
| 1 |
| 3 |
∴h=
| 3 |
练习册系列答案
53天天练系列答案
相关题目
如图，在棱长为2的正方体ABCD-A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1、AD的中点，那么异面直线OE和FD1所成的角的余弦值等于（ ）在棱长为2的正方体AC1中，G是AA1的中点，则BD到平面GB1D1的距离是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（理科）如图，在棱长为1的正方体A'C中，过BD及B'C'的中点E作截面BEFD交C'D'于F．
（2007•上海）如图，在棱长为2的正方体ABCD-A'B'C'D'中，E，F分别是A'B'和AB的中点，求异面直线A'F与CE所成角的大小 （结果用反三角函数值表示）．
中，点E，F分别是棱AB，BC的中点，则点
到平面
EF的距离是
