题目内容
已知圆心C在直线x+2y=0上,与x轴相切于x轴下方,且截直线x+y=0所得弦长为2
.
(1)求圆C的方程;
(2)若圆C与圆E:x2+(y-1)2=r2(r>0)相切,求r的值;
(3)若直线y=kx与圆C交于M,N两点,O为坐标原点,求
•
的值.
| 2 |
(1)求圆C的方程;
(2)若圆C与圆E:x2+(y-1)2=r2(r>0)相切,求r的值;
(3)若直线y=kx与圆C交于M,N两点,O为坐标原点,求
| OM |
| ON |
分析:(1)利用垂径定理及圆的半径r、弦心距d、弦长l三者之间的关系r2=d2+(
)2可得r,即可;
(2)利用两圆相切的性质即可得出;
(3)利用数量积及其切割线定理即可.
| l |
| 2 |
(2)利用两圆相切的性质即可得出;
(3)利用数量积及其切割线定理即可.
解答:解:(1)设圆心C(-2a,a),则半径r=|a|.
点C到x+y=0的距离d=
.所以|a|2=(
)2+(
)2,解得a2=4,a=-2.
故圆方程为(x-4)2+(y+2)2=4.
(2)由C(4,-2),r1=2,E(0,1).则|CE|=5.
当圆C与圆E外切时,r+2=5,r=3;
当圆C与圆E内切时,|r-2|=5,r=7.
所以r=3或r=7.
(3)设圆C与x轴切于点P.
则
•
=|
| |
|cos0=|
| |
|=|
|2=16.
点C到x+y=0的距离d=
| |-2a+a| | ||
|
| 2 |
| |a| | ||
|
故圆方程为(x-4)2+(y+2)2=4.
(2)由C(4,-2),r1=2,E(0,1).则|CE|=5.
当圆C与圆E外切时,r+2=5,r=3;
当圆C与圆E内切时,|r-2|=5,r=7.
所以r=3或r=7.
(3)设圆C与x轴切于点P.
则
| OM |
| ON |
| OM |
| ON |
| OM |
| ON |
| OP |
点评:熟练掌握圆的性质及其标准方程、垂径定理及圆的半径r、弦心距d、弦长l三者之间的关系r2=d2+(
)2、两圆相切的性质、数量积及其切割线定理等是解题的关键.
| l |
| 2 |

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
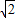 .
.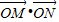 的值.
的值.