题目内容
已知⊙C与两平行直线x-y=0及x-y-4=0都相切,且圆心C在直线x+y=0上,
(Ⅰ)求⊙C的方程;
(Ⅱ)斜率为2的直线l与⊙C相交于A,B两点,O为坐标原点且满足
⊥
,求直线l的方程.
(Ⅰ)求⊙C的方程;
(Ⅱ)斜率为2的直线l与⊙C相交于A,B两点,O为坐标原点且满足
| OA |
| OB |
分析:(Ⅰ)利用平行线之间的距离求出圆的直径,设出圆心坐标,利用圆心到直线的距离,求出圆心坐标,可得圆的方程.
(Ⅱ)利用(Ⅰ)的结论,说明直线l经过圆的圆心,然后利用两点式求出直线方程即可.
(Ⅱ)利用(Ⅰ)的结论,说明直线l经过圆的圆心,然后利用两点式求出直线方程即可.
解答:解:(Ⅰ)由题意知⊙C的直径为两平行线 x-y=0及x-y-4=0之间的距离
∴d=2R=
=2
解得R=
,…(3分)
由圆心C(a,-a)到 x-y=0的距离
=R=
得a=±1,检验得a=1…(6分)
∴⊙C的方程为(x-1)2+(y+1)2=2…(7分)
(Ⅱ)由(Ⅰ)知⊙C过原点,因为
⊥
,则l经过圆心,…(9分)
直线l的斜率为:2,圆的圆心坐标(1,-1),
所以直线l的方程:2x-y-3=0…(13分)
(注:其它解法请参照给分.)
∴d=2R=
| |0-(-4)| | ||
|
| 2 |
| 2 |
由圆心C(a,-a)到 x-y=0的距离
| |2a| | ||
|
| 2 |
∴⊙C的方程为(x-1)2+(y+1)2=2…(7分)
(Ⅱ)由(Ⅰ)知⊙C过原点,因为
| OA |
| OB |
直线l的斜率为:2,圆的圆心坐标(1,-1),
所以直线l的方程:2x-y-3=0…(13分)
(注:其它解法请参照给分.)
点评:本题考查圆的标准方程的求法,直线与圆的位置关系,考查计算能力与转化思想的应用.

练习册系列答案
相关题目
 ,求直线l的方程.
,求直线l的方程.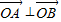 ,求直线l的方程.
,求直线l的方程.