题目内容
(2005•普陀区一模)在圆x2+y2=4上与直线4x+3y-12=0距离最小的点的坐标是
(
,
)
| 8 |
| 5 |
| 6 |
| 5 |
(
,
)
.| 8 |
| 5 |
| 6 |
| 5 |
分析:若把直线4x+3y-12=0向圆平行移动,成为圆的切线时,切点到直线4x+3y-12=0距离最小,所以圆心与直到线4x+3y-12=0距离最小的点连线垂直于直线4x+3y-12=0,只需求出过圆心的直线4x+3y-12=0的垂线方程,与圆方程联立,解出交点,即为所求.
解答:解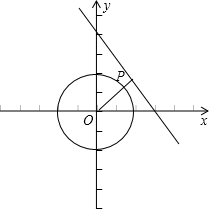 :过圆心O向直线4x+3y-12=0作垂线OP,与圆交于点P,则P点到直线距离最小.
:过圆心O向直线4x+3y-12=0作垂线OP,与圆交于点P,则P点到直线距离最小.
∵OP垂直于直线4x+3y-12=0,∴斜率为
∴OP的方程为y=
x
由
,得,x=
,y=
或x=-
,y=-
舍去.
故答案为(
,
)
 :过圆心O向直线4x+3y-12=0作垂线OP,与圆交于点P,则P点到直线距离最小.
:过圆心O向直线4x+3y-12=0作垂线OP,与圆交于点P,则P点到直线距离最小.∵OP垂直于直线4x+3y-12=0,∴斜率为
| 3 |
| 4 |
∴OP的方程为y=
| 3 |
| 4 |
由
|
| 8 |
| 5 |
| 6 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
故答案为(
| 8 |
| 5 |
| 6 |
| 5 |
点评:本题主要考查了直线与圆的位置关系的判断,其中综合考查了学生的理解力与转化的能力.

练习册系列答案
相关题目