题目内容
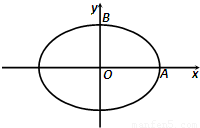
如图,焦距为2的椭圆E的两个顶点分别为A和B,且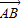 与
与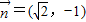 共线.
共线.(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线y=kx+m与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
【答案】分析:(Ⅰ)设椭圆E的标准方程为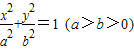 ,由A(a,0)、B(0,b),知
,由A(a,0)、B(0,b),知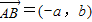 ,由
,由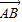 与
与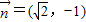 共线,知
共线,知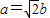 ,由此能求出椭圆E的标准方程.
,由此能求出椭圆E的标准方程.
(Ⅱ)设P(x1,y1),Q(x2,y2),把直线方程y=kx+m代入椭圆方程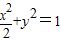 ,得(2k2+1)x2+4kmx+2m2-2=0,故
,得(2k2+1)x2+4kmx+2m2-2=0,故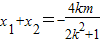 ,
,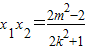 ,△=16k2m2-4×(2k2+1)(2m2-2)=16k2-8m2+8>0,由此能求出实数m的取值范围.
,△=16k2m2-4×(2k2+1)(2m2-2)=16k2-8m2+8>0,由此能求出实数m的取值范围.
解答:解:(Ⅰ)设椭圆E的标准方程为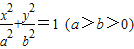 ,
,
由已知得A(a,0)、B(0,b),
∴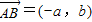 ,
,
∵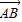 与
与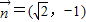 共线,
共线,
∴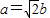 ,又a2-b2=1(3分)
,又a2-b2=1(3分)
∴a2=2,b2=1,
∴椭圆E的标准方程为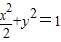 (5分)
(5分)
(Ⅱ)设P(x1,y1),Q(x2,y2),
把直线方程y=kx+m代入椭圆方程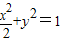 ,
,
消去y,得,(2k2+1)x2+4kmx+2m2-2=0,
∴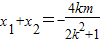 ,
,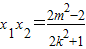 (7分)
(7分)
△=16k2m2-4×(2k2+1)(2m2-2)=16k2-8m2+8>0(*) (8分)
∵原点O总在以PQ为直径的圆内,
∴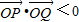 ,即x1x2+y1y2<0(9分)
,即x1x2+y1y2<0(9分)
又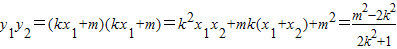
由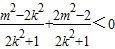 得
得 ,
,
依题意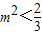 且满足(*) (11分)
且满足(*) (11分)
故实数m的取值范围是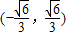 (12分)
(12分)
点评:本题考查椭圆参数方程的求法,考实数的取值范围,考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
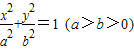 ,由A(a,0)、B(0,b),知
,由A(a,0)、B(0,b),知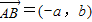 ,由
,由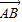 与
与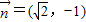 共线,知
共线,知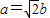 ,由此能求出椭圆E的标准方程.
,由此能求出椭圆E的标准方程.(Ⅱ)设P(x1,y1),Q(x2,y2),把直线方程y=kx+m代入椭圆方程
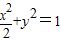 ,得(2k2+1)x2+4kmx+2m2-2=0,故
,得(2k2+1)x2+4kmx+2m2-2=0,故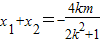 ,
,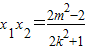 ,△=16k2m2-4×(2k2+1)(2m2-2)=16k2-8m2+8>0,由此能求出实数m的取值范围.
,△=16k2m2-4×(2k2+1)(2m2-2)=16k2-8m2+8>0,由此能求出实数m的取值范围.解答:解:(Ⅰ)设椭圆E的标准方程为
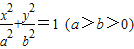 ,
,由已知得A(a,0)、B(0,b),
∴
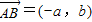 ,
,∵
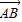 与
与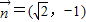 共线,
共线,∴
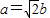 ,又a2-b2=1(3分)
,又a2-b2=1(3分)∴a2=2,b2=1,
∴椭圆E的标准方程为
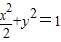 (5分)
(5分)(Ⅱ)设P(x1,y1),Q(x2,y2),
把直线方程y=kx+m代入椭圆方程
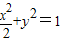 ,
,消去y,得,(2k2+1)x2+4kmx+2m2-2=0,
∴
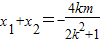 ,
,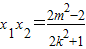 (7分)
(7分)△=16k2m2-4×(2k2+1)(2m2-2)=16k2-8m2+8>0(*) (8分)
∵原点O总在以PQ为直径的圆内,
∴
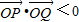 ,即x1x2+y1y2<0(9分)
,即x1x2+y1y2<0(9分)又
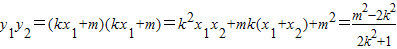
由
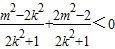 得
得 ,
,依题意
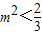 且满足(*) (11分)
且满足(*) (11分)故实数m的取值范围是
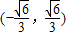 (12分)
(12分)点评:本题考查椭圆参数方程的求法,考实数的取值范围,考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
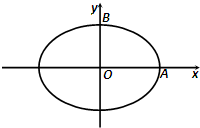 (2012•河南模拟)如图,焦距为2的椭圆E的两个顶点分别为A和B,且
(2012•河南模拟)如图,焦距为2的椭圆E的两个顶点分别为A和B,且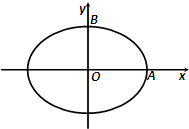 如图,焦距为2的椭圆D的两个顶点分别为A和B,且
如图,焦距为2的椭圆D的两个顶点分别为A和B,且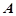 和
和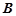 ,且
,且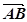 与
与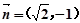 共线.
共线.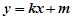 与椭圆E有两个不同的交
与椭圆E有两个不同的交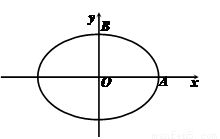
 和
和 ,且
,且 与
与 共线.
共线. 与椭圆E有两个不同的交
与椭圆E有两个不同的交
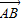 与
与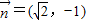 共线.
共线.