题目内容
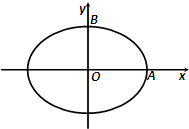 如图,焦距为2的椭圆D的两个顶点分别为A和B,且
如图,焦距为2的椭圆D的两个顶点分别为A和B,且| AB |
| n |
| 2 |
(Ⅰ)求椭圆D的标准方程;
(Ⅱ)过点M(0,m)且斜率为
| 2 |
分析:(Ⅰ)设椭圆E的标准方程为
+
=1 (a>b>0),由已知得A(a,0)、B(0,b),故
=(-a,b),由
与
=(
,-1)共线,知a=
b,由此能求出椭圆E的标准方程.
(Ⅱ)设P(x1,y1),Q(x2,y2),把直线方程y=
x+m代入椭圆方程
+y2=1,得,5x2+4
mx+2m2-2=0,故x1+x2=-
,x1x2=
,△=32m2-20(2m2-2)=-8m2+40>0,故m2<5.由以PQ为直径的圆经过原点O知
•
=0,由此能求出实数m的值.
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| AB |
| n |
| 2 |
| 2 |
(Ⅱ)设P(x1,y1),Q(x2,y2),把直线方程y=
| 2 |
| x2 |
| 2 |
| 2 |
4
| ||
| 5 |
| 2m2-2 |
| 5 |
| OP |
| OQ |
解答:解:(Ⅰ)设椭圆E的标准方程为
+
=1 (a>b>0),
由已知得A(a,0)、B(0,b),
∴
=(-a,b),
∵
与
=(
,-1)共线,
∴a=
b,又a2-b2=1(3分)
∴a2=2,b2=1,
∴椭圆E的标准方程为
+y2=1(5分)
(Ⅱ)设P(x1,y1),Q(x2,y2),
把直线方程y=
x+m代入椭圆方程
+y2=1,
消去y,得,5x2+4
mx+2m2-2=0,
∴x1+x2=-
,x1x2=
(7分)
△=32m2-20(2m2-2)=-8m2+40>0,
∴m2<5(8分)
∵以PQ为直径的圆经过原点O,
∴
•
=0,即x1x2+y1y2=0(9分)
又y1y2=(
x1+m)(
x1+m)=2x1x2+
m(x1+x2)+m2=
-
+m2
由x1x2+y1y2=0得
=0,
∴m2=2<5(11分)
∴m=±
(12分)
| x2 |
| a2 |
| y2 |
| b2 |
由已知得A(a,0)、B(0,b),
∴
| AB |
∵
| AB |
| n |
| 2 |
∴a=
| 2 |
∴a2=2,b2=1,
∴椭圆E的标准方程为
| x2 |
| 2 |
(Ⅱ)设P(x1,y1),Q(x2,y2),
把直线方程y=
| 2 |
| x2 |
| 2 |
消去y,得,5x2+4
| 2 |
∴x1+x2=-
4
| ||
| 5 |
| 2m2-2 |
| 5 |
△=32m2-20(2m2-2)=-8m2+40>0,
∴m2<5(8分)
∵以PQ为直径的圆经过原点O,
∴
| OP |
| OQ |
又y1y2=(
| 2 |
| 2 |
| 2 |
| 4m2-4 |
| 5 |
| 8m2 |
| 5 |
由x1x2+y1y2=0得
| 4m2-4-8m2+5m2+2m2-2 |
| 5 |
∴m2=2<5(11分)
∴m=±
| 2 |
点评:本题考查椭圆标准方程的求法和求实数的值,综合性强,难度大,是高考的重点,解题时要认真审题,仔细解答.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
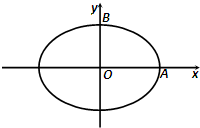 (2012•河南模拟)如图,焦距为2的椭圆E的两个顶点分别为A和B,且
(2012•河南模拟)如图,焦距为2的椭圆E的两个顶点分别为A和B,且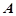 和
和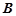 ,且
,且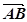 与
与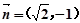 共线.
共线.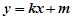 与椭圆E有两个不同的交
与椭圆E有两个不同的交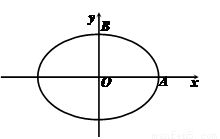
 和
和 ,且
,且 与
与 共线.
共线. 与椭圆E有两个不同的交
与椭圆E有两个不同的交
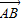 与
与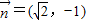 共线.
共线.