题目内容
正三棱锥P-ABC底面正三角形的边长为1,其外接球球心O为△ABC的重心,则此正三棱锥的体积为
.
| 1 |
| 12 |
| 1 |
| 12 |
分析:由题意求出底面面积及三棱锥S-ABC的高,然后求出三棱锥的体积.
解答: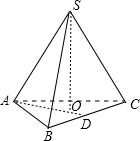 解:三棱锥S-ABC中,PO⊥底面ABC,
解:三棱锥S-ABC中,PO⊥底面ABC,
底面ABC是边长为1正三角形,所以底面面积为:
×AB2=
×12=
,
三角形ABC中,O是其中心,也是球心,
∴AO=
AD=
×
×1=
即三棱锥S-ABC的高SO=AO=
,
棱锥的体积为:
×
×
=
.
故答案为:
.
 解:三棱锥S-ABC中,PO⊥底面ABC,
解:三棱锥S-ABC中,PO⊥底面ABC,底面ABC是边长为1正三角形,所以底面面积为:
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
三角形ABC中,O是其中心,也是球心,
∴AO=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
即三棱锥S-ABC的高SO=AO=
| ||
| 3 |
棱锥的体积为:
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| 1 |
| 12 |
故答案为:
| 1 |
| 12 |
点评:本题是基础题,考查球内接多面体、三棱锥的体积的计算,注意三棱锥的特征是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
设O是正三棱锥P-ABC底面是三角形ABC的中心,过O的动平面与PC交于S,与PA、PB的延长线分别交于Q、R,则和式
+
+
( )
| 1 |
| PQ |
| 1 |
| PR |
| 1 |
| PS |
| A、有最大值而无最小值 |
| B、有最小值而无最大值 |
| C、既有最大值又有最小值,两者不等 |
| D、是一个与面QPS无关的常数 |