题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)设![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(Ⅲ)设![]() 是
是![]() 的两个零点,证明
的两个零点,证明![]() .
.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(Ⅱ)当
上单调递增;(Ⅱ)当![]() 时,
时,![]() ;(Ⅲ)证明过程见解析
;(Ⅲ)证明过程见解析
【解析】试题分析:(Ⅰ)求导,并判断导数的符号,分别讨论![]() 的取值,确定函数的单调区间.
的取值,确定函数的单调区间.
(Ⅱ)构造函数![]() ,利用导数求函数
,利用导数求函数![]() 当
当![]() 时的最大值小于零即可.
时的最大值小于零即可.
(Ⅲ)由(Ⅱ)得![]() ,从而
,从而![]() ,于是
,于是![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() .
.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,
求导数,得![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() 在
在![]() 上单调递增,
上单调递增,
若![]() ,则由
,则由![]() 得
得![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
此时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)令![]() ,则
,则

![]() .
.
求导数,得![]() ,
,
当时![]() ,
,![]() ,
,![]() 在
在![]() 上是减函数.
上是减函数.
而![]() ,
,![]() ,
,
故当![]() 时,
时,![]()
(Ⅲ)由(Ⅰ)可知,当![]() 时,函数
时,函数![]() 至多有一个零点,
至多有一个零点,
故![]() ,从而
,从而![]() 的最小值为
的最小值为![]() ,且
,且![]() ,
,
不妨设![]() ,则
,则![]() ,
,![]() ,
,
由(Ⅱ)得![]() ,
,
从而![]() ,于是
,于是![]() ,
,
由(Ⅰ)知,![]() .
.
点晴:本题考查函数导数的单调性.不等式比较大小,函数的零点问题:在(Ⅰ)中通过求导,并判断导数的符号,分别讨论![]() 的取值,确定函数的单调区间.(Ⅱ)通过构造函数
的取值,确定函数的单调区间.(Ⅱ)通过构造函数![]() ,把不等式证明问题转化为函数求最值问题,求函数
,把不等式证明问题转化为函数求最值问题,求函数![]() 当
当![]() 时的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)问的结论.
时的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)问的结论.

练习册系列答案
相关题目
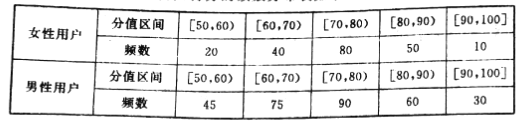
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数),现随机抽取20天的指数(见下表),将指数不低于![]() 视为当天空气质量优良.
视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
(1)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(2)以这20天的数据估计我市总体空气质量(天数很多),若从我市总体空气质量指数中随机抽取3天的指数,用![]() 表示抽到空气质量为优良的天数,求
表示抽到空气质量为优良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.