题目内容
(本题满分12分)为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
|
分组 |
频数 |
频率 |
|
60.5~70.5 |
|
0.16 |
|
70.5~80.5 |
10 |
|
|
80.5~90.5 |
18 |
0.36 |
|
90.5~100.5 |
|
|
|
合计 |
50 |
|
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
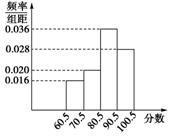
(2)填充频率分布表的空格(将答案直接填在表格内),并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
(1)编号为016. ------3分
|
分组 |
频数 |
频率 |
|
60.5~70.5 |
8 |
0.16 |
|
70.5~80.5 |
10 |
0.20 |
|
80.5~90.5 |
18 |
0.36 |
|
90.5~100.5 |
14 |
0.28 |
|
合计 |
50 |
1 |
(2)
 |
(3)在被抽到的学生中获二等奖的人数9+7=16(人),占样本的比例是=0.32,即获二等奖的概率为32%,所以获二等奖的人数估计为800×32%=256(人).
答:获二等奖的大约有256人.
【解析】略

(本题满分12分)
为迎接国庆60周年,美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示。要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?w.w.w.k.s.5.u.c.o.m ![]()
|
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(本题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中,![]() 还喜欢打羽毛球,
还喜欢打羽毛球,![]() 还喜欢打乒乓球,
还喜欢打乒乓球,![]() 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)![]()
(本题满分12分)
为预防 病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
|
|
A组 |
B组 |
C组 |
|
疫苗有效 |
673 |
|
|
|
疫苗无效 |
77 |
90 |
|
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知 ,求不能通过测试的概率.
,求不能通过测试的概率.



 、
、 、
、 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出 、
、 ,求事件“
,求事件“ ”的概率.
”的概率.
 为实数,函数
为实数,函数 .
.  ,求
,求 的最小值;
的最小值;  ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式 的解集.
的解集.