题目内容
设实数a≠0,数列{an}是首项为a,公比为-a的等比数列,记bn=anlg|an|(n∈N *),Sn=b1+b2+…+bn.
求证:当a≠-1时,对任意自然数n都有Sn=![]()
证明:∵an=a1qn-1=a(-a)n-1=(-1) n-1an,∴bn=anlg|an|?
=(-1) n-1anlg|(-1) n-1an|?
=(-1) n-1nanlg|a|,?
∴Sn=alg|a|-2a2lg|a|+3a3lg|a|+…+(-1) n-2(n-1)a n-1lg|a|+(-1) n-1nanlg|a|
=[a-2a2+3a3+…+(-1) n-2(n-1)·a n-1+(-1) n-1nan]lg|a|.
记S=a-2a2+3a3+…+(-1) n-2·(n-1)a n-1+(-1) n-1nan,①
aS=a2-2a3+…+(-1) n-3(n-2)a n-1+(-1) n-2(n-1)an+(-1) n-1na n+1,②
①+②得(1+a)S=a-a2+a3+…+(-1) n-2an-1+(-1)n-2an+(-1) n-1na n+1.③
∵a≠-1,
∴(1+a)S=a+(-1) n-1a n+1![]()
∴S=![]()
∴Sn=![]()

练习册系列答案
相关题目
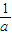 )有最小值-1.
)有最小值-1. ,证明:数列{bn}是等差数列.
,证明:数列{bn}是等差数列.