题目内容
设实数a≠0,函数f(x)=a(x2+1)-(2x+| 1 |
| a |
(1)求a的值;
(2)设数列{an}的前n项和Sn=f(n),令bn=
| a2+a4+…+a2n |
| n |
分析:由f(x)=a(x-
)2+a-
有最小值-1可得,f(
)=a-
=-1,且a>0,解方程可求
(2)由Sn=n2-2n可求a1=S1=-1.
当n≥2时,利用递推公式an=Sn-Sn-1=可求an,代入计算a2+a4+…+a2n=n(2n-1)从而可得,bn=
=2n-1.
要证数列{bn}是等差数列?bn+1-bn=d即可
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
(2)由Sn=n2-2n可求a1=S1=-1.
当n≥2时,利用递推公式an=Sn-Sn-1=可求an,代入计算a2+a4+…+a2n=n(2n-1)从而可得,bn=
| n(2n-1) |
| n |
要证数列{bn}是等差数列?bn+1-bn=d即可
解答:(1)解:∵f(x)=a(x-
)2+a-
,由已知知f(
)=a-
=-1,且a>0,解得a=1,a=-2(舍去).
(2)证明:由(1)得f(x)=x2-2x,
∴Sn=n2-2n,a1=S1=-1.
当n≥2时,an=Sn-Sn-1=n2-2n-(n-1)2+2(n-1)=2n-3,a1满足上式即an=2n-3.
∵an+1-an=2(n+1)-3-2n+3=2,
∴数列{an}是首项为-1,公差为2的等差数列.
∴a2+a4+…+a2n=
=
=n(2n-1),
即bn=
=2n-1.
∴bn+1-bn=2(n+1)-1-2n+1=2.
又b2=
=1,
∴{bn}是以1为首项,2为公差的等差数列.
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
(2)证明:由(1)得f(x)=x2-2x,
∴Sn=n2-2n,a1=S1=-1.
当n≥2时,an=Sn-Sn-1=n2-2n-(n-1)2+2(n-1)=2n-3,a1满足上式即an=2n-3.
∵an+1-an=2(n+1)-3-2n+3=2,
∴数列{an}是首项为-1,公差为2的等差数列.
∴a2+a4+…+a2n=
| n(a2+a2n) |
| 2 |
=
| n(1+4n-3) |
| 2 |
即bn=
| n(2n-1) |
| n |
∴bn+1-bn=2(n+1)-1-2n+1=2.
又b2=
| a2 |
| 1 |
∴{bn}是以1为首项,2为公差的等差数列.
点评:(1)考查了在数列中利用二次函数求解最值属于数列与函数简单综合(2)考查了利用递推公式由Sn求an,要注意对n=1时的项是否适合通项的检验,还考查了利用定义证明等差数列.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )有最小值-1.
)有最小值-1.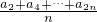 ,证明:数列{bn}是等差数列.
,证明:数列{bn}是等差数列.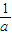 )有最小值-1.
)有最小值-1. ,证明:数列{bn}是等差数列.
,证明:数列{bn}是等差数列.