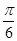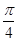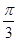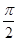题目内容
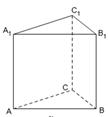
已知三棱柱 中,平面
中,平面 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
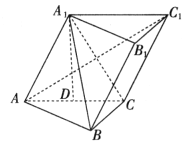
(Ⅰ)求证:AC1⊥平面A1BC;
(Ⅱ)求平面AA1B与平面A1BC的夹角的余弦值。
 中,平面
中,平面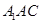 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
(Ⅰ)求证:AC1⊥平面A1BC;
(Ⅱ)求平面AA1B与平面A1BC的夹角的余弦值。
(Ⅰ)详见解析;(Ⅱ)平面AA1B与平面A1BC的夹角的余弦值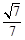 .
.
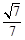 .
.试题分析:(Ⅰ)求证:AC1⊥平面A1BC,只需证
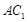 垂直平面
垂直平面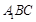 内两条线即可,由于平面
内两条线即可,由于平面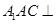 平面
平面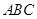 ,
, ,可得
,可得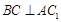 ,由题意可得,四边形
,由题意可得,四边形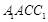 是菱形,由菱形对角线性质可知,
是菱形,由菱形对角线性质可知,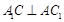 ,从而可得
,从而可得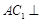 平面
平面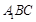 ,也可利用向量法,即如图以
,也可利用向量法,即如图以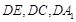 为
为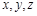 轴建立空间直角坐标系,由
轴建立空间直角坐标系,由
 知
知 ,即可得
,即可得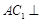 平面
平面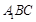 ;(Ⅱ)求平面AA1B与平面A1BC的夹角的余弦值,可用传统方法,找二面角的平面角,设
;(Ⅱ)求平面AA1B与平面A1BC的夹角的余弦值,可用传统方法,找二面角的平面角,设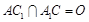 ,作
,作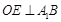 于
于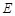 ,连接
,连接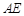 ,则
,则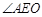 为二面角的平面角,从而求得两平面夹角的余弦值为
为二面角的平面角,从而求得两平面夹角的余弦值为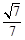 ,还可以利用向量来求,即找出两个平面的法向量,利用法向量的夹角平面AA1B与平面A1BC的夹角的余弦值.
,还可以利用向量来求,即找出两个平面的法向量,利用法向量的夹角平面AA1B与平面A1BC的夹角的余弦值.试题解析:解法一:
(Ⅰ)由于平面
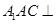 平面
平面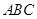 ,
, ,所以
,所以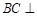 面
面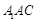 ,所以
,所以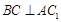 。(2分)
。(2分)而
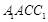 是菱形,因此
是菱形,因此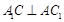 ,所以
,所以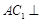 平面
平面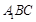 。(4分)
。(4分)(Ⅱ)设
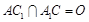 ,作
,作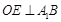 于
于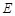 ,连接
,连接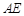 ,
,由(1)知
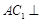 平面
平面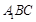 ,即
,即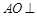 平面
平面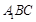 ,所以
,所以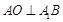
又
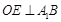 于
于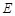 ,因此
,因此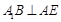 ,
,所以
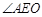 为二面角的平面角
为二面角的平面角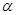 ,(8分)
,(8分)在
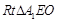 中,
中,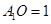 ,
,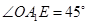 ,故直角边
,故直角边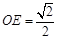 ,
,又因为
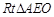 中斜边
中斜边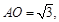 因此
因此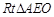 中斜边
中斜边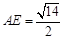 ,
,所以
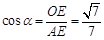 ,所以所求两平面夹角的余弦值为
,所以所求两平面夹角的余弦值为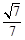 。(12分)
。(12分)解法二:
如图,取
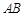 的中点
的中点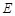 ,则
,则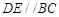 ,
,
因为
 ,所以
,所以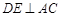 ,又
,又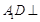 平面
平面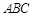 ,(2分)
,(2分)以
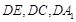 为
为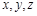 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则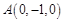 ,
,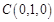 ,
,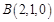 ,
,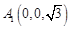 ,
,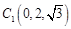 ,
,(Ⅰ)
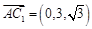 ,
,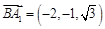 ,
,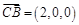 ,
,
由

 知
知 , (5分)
, (5分)又
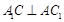 ,从而
,从而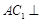 平面
平面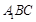 ;(6分)
;(6分)(Ⅱ)由(1)知平面
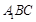 的一个法向量为
的一个法向量为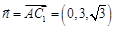 ,
,再设平面
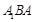 的法向量为
的法向量为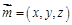 ,
,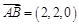 ,
, ,
, 所以
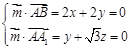 ,设
,设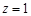 ,则
,则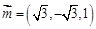 ,
, 故
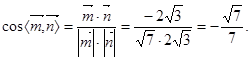
因此所求两平面夹角的余弦值为
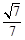 。(12分)
。(12分)
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
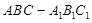 中,
中,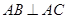 ,
,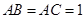 ,
,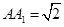 ,D为BC中点.
,D为BC中点.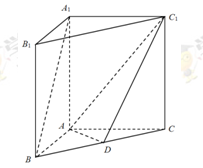
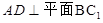 ;
; ;
;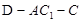 的正弦值.
的正弦值.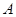 、
、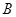 、
、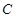 为不在同一直线上的三点,且
为不在同一直线上的三点,且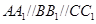 ,
,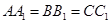 .
.
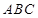 //平面
//平面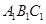 ;
;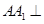 平面
平面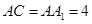 ,
,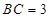 ,
,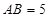 ,求证:
,求证: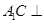 平面
平面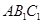 ;
;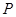 为
为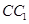 上的动点,求当
上的动点,求当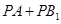 取得最小值时
取得最小值时 的长.
的长.

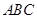 的直角边
的直角边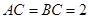 ,沿其中位线
,沿其中位线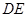 将平面
将平面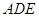 折起,使平面
折起,使平面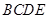 ,得到四棱锥
,得到四棱锥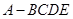 ,设
,设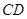 、
、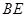 、
、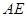 、
、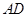 的中点分别为
的中点分别为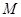 、
、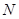 、
、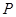 、
、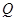 .
.


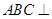 平面
平面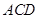 ;
;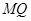 所成的角.
所成的角. 中,
中, 分别是
分别是 的中点,则四边形
的中点,则四边形 是( )
是( )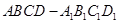 的棱长为
的棱长为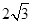 ,动点P在对角线
,动点P在对角线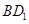 上,过点P作垂直于
上,过点P作垂直于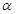 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设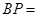 x,则当
x,则当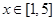 时,函数
时,函数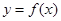 的值域为( )
的值域为( )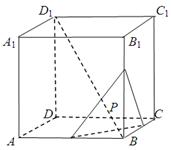
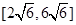
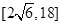
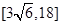
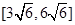
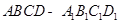 中,
中,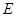 ,
,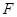 分别为棱
分别为棱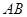 ,
,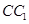 的中点,在平面
的中点,在平面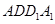 内且与平面
内且与平面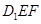 平行的直线( )
平行的直线( )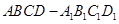 中,
中,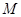 、
、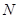 分别是
分别是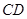 、
、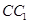 的中点,则异面直线
的中点,则异面直线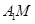 与
与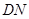 所成角的大小是( )
所成角的大小是( )