题目内容
已知函数 (
(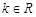 ).
).
(1)若函数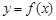 在
在 处取得极大值,求
处取得极大值,求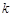 的值;
的值;
(2)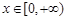 时,函数
时,函数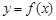 图象上的点都在
图象上的点都在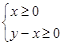 所表示的区域内,求
所表示的区域内,求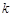 的取值范围;
的取值范围;
(3)证明: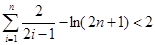 ,
,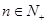 .
.
 (
(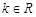 ).
).(1)若函数
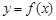 在
在 处取得极大值,求
处取得极大值,求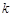 的值;
的值;(2)
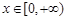 时,函数
时,函数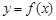 图象上的点都在
图象上的点都在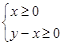 所表示的区域内,求
所表示的区域内,求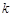 的取值范围;
的取值范围;(3)证明:
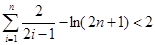 ,
,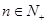 .
.(1) 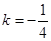 ;(2)
;(2) 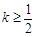 .
.
(3)数学归纳法可知, ,
,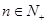 。
。
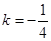 ;(2)
;(2) 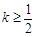 .
. (3)数学归纳法可知,
 ,
,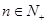 。
。试题分析:(1)
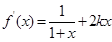 ,由
,由 经检验符合题意 (3分)
经检验符合题意 (3分)(2)依题意知,不等式
 在
在 恒成立.令
恒成立.令 ,
,当k≤0时,取x=1,有
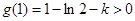 ,故k≤0不合.(4分)
,故k≤0不合.(4分)当k>0时, g′(x)=
 -2kx=
-2kx=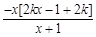 .
.令g′(x)=0,得x1=0,x2=
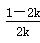 >-1. (5分)
>-1. (5分)①当k≥
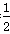 时,
时,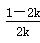 ≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减,从而对任意的x∈[0,+∞),总有g(x)≤g(0)=0,故k≥
≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减,从而对任意的x∈[0,+∞),总有g(x)≤g(0)=0,故k≥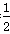 符合题意,6分②当0<k<
符合题意,6分②当0<k<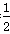 时,
时,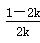 >0, 对于x∈
>0, 对于x∈ ,g′(x)>0,
,g′(x)>0,故g(x)在
 内单调递增,因此当取x0∈
内单调递增,因此当取x0∈ 时,g(x0)>g(0)=0,不合.
时,g(x0)>g(0)=0,不合.综上,
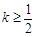 . (8分)
. (8分)(3)证明:当n=1时,不等式左边=2-ln3<2=右边,所以不等式成立.(9分)
当n≥2时,在(2)中取k=
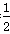 ,得
,得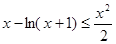 (10分)
(10分)取
 代入上式得:
代入上式得: 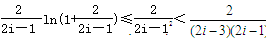 (12分)
(12分)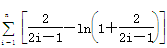 ≤2-ln3+
≤2-ln3+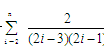
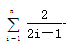 -ln(2n+1)≤2-ln3+1-
-ln(2n+1)≤2-ln3+1-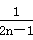 <2.
<2.综上,
 ,
,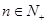 (14分)
(14分)点评:难题,本题属于导数应用中的常见问题,(2)是恒成立问题,注意通过构造函数,研究函数的最值达到解题目的。(3)利用数学归纳法。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
相关题目
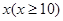 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为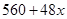 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)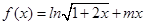 .
.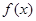 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数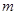 的取值范围;
的取值范围;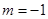 时,求函数
时,求函数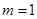 时,且
时,且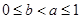 ,证明:
,证明: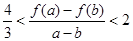 .
.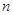 个月的维修费为
个月的维修费为 元,买这种冰激凌机花费
元,买这种冰激凌机花费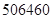 元,使用
元,使用 年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( )
年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( ) 机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;
机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗; 一年按
一年按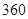 天计算.)
天计算.)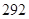 元
元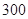 元
元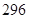 元
元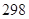 元
元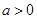 ,函数
,函数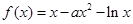 .
.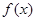 是单调函数,求实数
是单调函数,求实数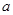 的取值范围;
的取值范围;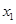 、
、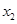 ,证明:
,证明: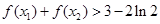 .
. ”表示一种运算,即:
”表示一种运算,即: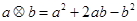 ,设函数
,设函数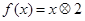 。且关于
。且关于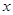 的方程为
的方程为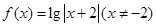 恰有四个互不相等的实数根
恰有四个互不相等的实数根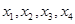 ,则
,则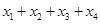 的值是( )
的值是( )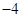
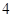
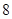

 的函数
的函数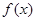 ,定义
,定义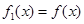 ,
,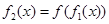 ,…,
,…,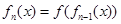 ,n=1,2,3,….满足
,n=1,2,3,….满足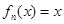 的点称为f的
的点称为f的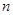 阶周期点.
阶周期点.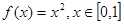 则f的
则f的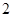 阶周期点的个数是___________;
阶周期点的个数是___________;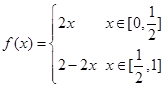 则f的
则f的 ,求
,求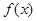 。
。