题目内容
设直线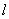 的方程为
的方程为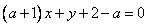
 。
。
(1) 若 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求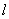 的方程;
的方程;
(2) 若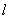 不经过第二象限,求a的取值范围。
不经过第二象限,求a的取值范围。
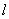 的方程为
的方程为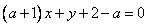
 。
。(1) 若
 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求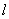 的方程;
的方程;(2) 若
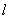 不经过第二象限,求a的取值范围。
不经过第二象限,求a的取值范围。 解:(1)由题意,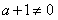 ,即
,即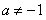 ,
,
当直线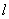 过原点时,该直线在两条坐标轴上的截距都0,显然相等,
过原点时,该直线在两条坐标轴上的截距都0,显然相等,
此时a=2,直线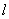 的方程为3x+y=0;
的方程为3x+y=0;
当直线 不过原点时,
不过原点时,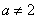 ,由截距相等,得
,由截距相等,得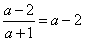 ,即a=0,
,即a=0,
直线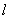 的方程为x+y+2=0,
的方程为x+y+2=0,
综上所述,所求直线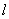 的方程为3x+y=0或x+y+2=0。
的方程为3x+y=0或x+y+2=0。
(2)将直线 的方程化为
的方程化为 ,
,
为使直线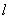 不经过第二象限,当且仅当
不经过第二象限,当且仅当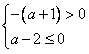 或
或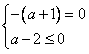 ,
,
解得: ,
,
所以,a的取值范围是 。
。
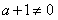 ,即
,即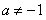 ,
,当直线
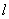 过原点时,该直线在两条坐标轴上的截距都0,显然相等,
过原点时,该直线在两条坐标轴上的截距都0,显然相等,此时a=2,直线
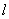 的方程为3x+y=0;
的方程为3x+y=0;当直线
 不过原点时,
不过原点时,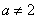 ,由截距相等,得
,由截距相等,得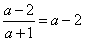 ,即a=0,
,即a=0,直线
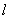 的方程为x+y+2=0,
的方程为x+y+2=0,综上所述,所求直线
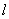 的方程为3x+y=0或x+y+2=0。
的方程为3x+y=0或x+y+2=0。(2)将直线
 的方程化为
的方程化为 ,
,为使直线
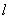 不经过第二象限,当且仅当
不经过第二象限,当且仅当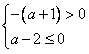 或
或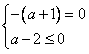 ,
,解得:
 ,
,所以,a的取值范围是
 。
。
练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
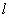 的方程为(a+1)x+y+2-a=0,(a
的方程为(a+1)x+y+2-a=0,(a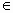 R),
R),
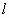 的方程为(a+1)x+y+2-a=0,(a
的方程为(a+1)x+y+2-a=0,(a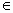 R),
R), 的方程为
的方程为
 。
。 的取值范围。
的取值范围。