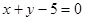题目内容
设直线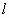 的方程为(a+1)x+y+2-a=0,(a
的方程为(a+1)x+y+2-a=0,(a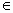 R),
R),
(1)若l在两坐标轴上的截距相等,求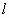 的方程;
的方程;
(2)若l不经过第二象限,求实数a的取值范围.
答案:略
解析:
提示:
解析:
|
(1) 若直线过原点,则在x轴、y轴上截距均为0,∴a=2,l的方程为3x+y=0;若直线不过原点,则 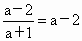 ,即a+1=1, ,即a+1=1,
∴ a=0.l 的方程为x+y+2=0.(2) 将l的方程化为y=-(a+1)x+a-2,要使l不经过第二象限,须 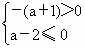 或 或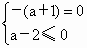
解得 a≤-1.可以结合图形得出条件,注意考虑特殊情况. 若直线 ax+by+c=0在第一、二、三象限,则[ ]
|
提示:
|
因为截距可以为零,所以求解时要展开讨论. |

练习册系列答案
相关题目
 的方程为(a+1)x+y+2-a=0,(a
的方程为(a+1)x+y+2-a=0,(a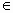 R),
R),
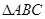 的一个顶点是
的一个顶点是
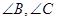 的平分线所在直线方程分别为
的平分线所在直线方程分别为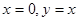 则直线
则直线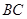 的方程为( )
的方程为( )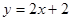 B.
B.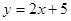 C.
C.
 D.
D.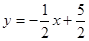
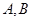 为
为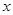 轴上两点,点
轴上两点,点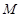 的横坐标为2,且
的横坐标为2,且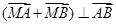 ,若直线
,若直线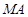 的方程为
的方程为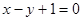 ,则直线
,则直线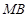 的方程为(
)
的方程为(
)
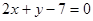 B.
B.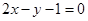
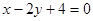 D.
D.