题目内容
2.对于任意实数k,直线(3k+2)x-ky-2=0与圆x2+y2-2x-2y-3=0的位置关系是相交.分析 根据圆的方程得到圆的半径,求出圆心到直线的距离d与半径r比较大小即可得到直线与圆的位置关系.
解答 解:把圆的方程化为标准形式得:(x-1)2+(y-1)2=5,可知圆的半径等于$\sqrt{5}$,
求出圆心到直线的距离d=$\frac{|2k|}{\sqrt{(3k+2)^{2}+{k}^{2}}}$≤2<$\sqrt{5}$,
所以直线与圆相交.
故答案为:相交.
点评 考查学生会用圆心到直线的距离与半径比较大小的方法判断直线与圆的位置关系,以及会利用点到直线的距离的距离公式.

练习册系列答案
相关题目
18.已知函数f(x)的定义域为R,且f(x)=f(-x),f(x+1)=-f(x),若f(x)在[-3,-2]上是减函数,$\frac{π}{4}$<α<β<$\frac{π}{2}$,则( )
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(tanα)>f(tanβ) | D. | 以上都不对 |
 ,则
,则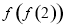 的值为( )
的值为( )