题目内容
(本小题满分14分)
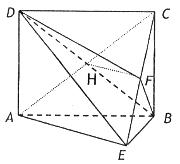
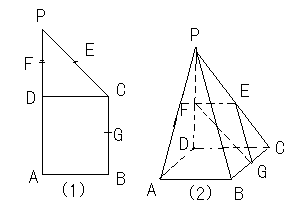
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.
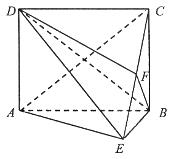
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.

(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD.
证明:见解析。
(I)证明:因为 即可.
即可.
(II)设BD与AC的交点为H,连接HF,则HF//AE,从而问题得证.
证明:
(1)AD⊥平面ABE,AE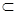 平面ABE,∴AD⊥AE,
平面ABE,∴AD⊥AE,
在矩形ABCD中,有AD∥BC,∴BC⊥AE.
∵BF⊥平面ACE,AE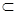 平面ABE,∴BF⊥AE,
平面ABE,∴BF⊥AE,
又∵BF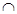 BC=B,BF,BC
BC=B,BF,BC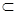 平面BCE,
平面BCE,
∴AE⊥平面BCE.(7分)
(2)设AC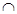 BD=H,连接HF,则H为AC的中点.
BD=H,连接HF,则H为AC的中点.
∵BF⊥平面ACE,CE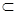 平面ABE,∴BF⊥CE,
平面ABE,∴BF⊥CE,
又因为AE=EB=BC,所以F为CE上的中点.
在△AEC中,FH为△AEC的中位线,则FH∥AE
又∵AE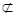 平面BFE,而FH
平面BFE,而FH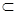 平面BFE
平面BFE
∴AE∥平面BFD.(14分)
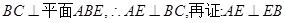 即可.
即可.(II)设BD与AC的交点为H,连接HF,则HF//AE,从而问题得证.
证明:
(1)AD⊥平面ABE,AE
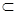 平面ABE,∴AD⊥AE,
平面ABE,∴AD⊥AE,在矩形ABCD中,有AD∥BC,∴BC⊥AE.
∵BF⊥平面ACE,AE
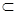 平面ABE,∴BF⊥AE,
平面ABE,∴BF⊥AE,又∵BF
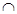 BC=B,BF,BC
BC=B,BF,BC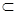 平面BCE,
平面BCE,∴AE⊥平面BCE.(7分)
(2)设AC
 BD=H,连接HF,则H为AC的中点.
BD=H,连接HF,则H为AC的中点.∵BF⊥平面ACE,CE
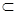 平面ABE,∴BF⊥CE,
平面ABE,∴BF⊥CE,又因为AE=EB=BC,所以F为CE上的中点.
在△AEC中,FH为△AEC的中位线,则FH∥AE
又∵AE
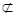 平面BFE,而FH
平面BFE,而FH 平面BFE
平面BFE∴AE∥平面BFD.(14分)


练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
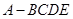 中,底面
中,底面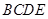 为矩形,侧面
为矩形,侧面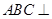 底面
底面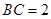 ,
,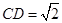 ,
,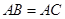 .
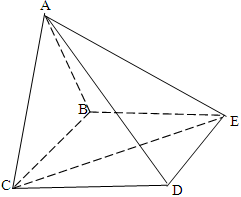
.
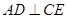 ;
; 与平面
与平面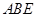 所成的角为
所成的角为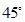 ,
, 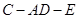 的余弦值.
的余弦值.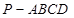 中,底面
中,底面 为平行四边形,
为平行四边形,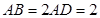 ,
,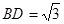 ,
,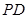 ⊥底面
⊥底面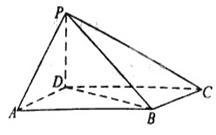
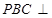 平面
平面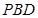 ;
; 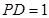 ,求
,求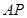 与平面
与平面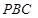 所成角
所成角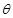 的正弦值.
的正弦值. 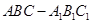 中,
中,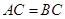 ,点
,点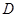 是
是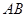 的中点,
的中点,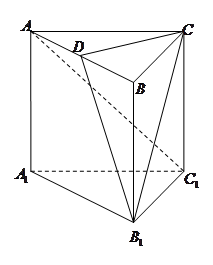
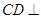 平面
平面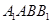 ;
;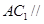 平面
平面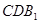
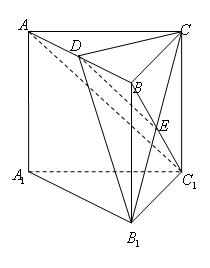
 是矩形,
是矩形,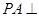 平面
平面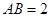 ,
,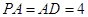 ,
,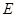 为
为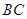 的中点.
的中点.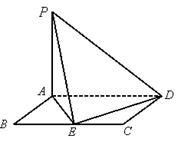
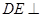 平面
平面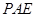 ;
;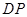 与平面
与平面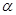 、
、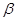 和直线
和直线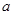 、
、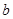 ,若
,若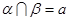 ,
,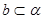 且
且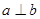 ,则
,则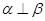 .
.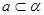 ,
,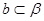 且
且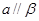 ,
,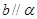 ,则
,则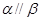 .
.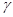 和直线
和直线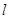 ,若
,若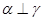 ,
,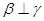 且
且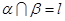 ,则
,则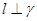 .
.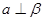 ,则
,则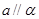 .
.
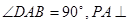
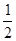 AB=1,M是PB的中点
AB=1,M是PB的中点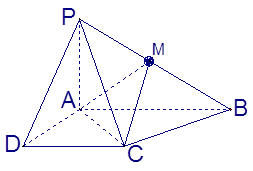
 ,
,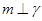 ,那么必有( )
,那么必有( )