题目内容
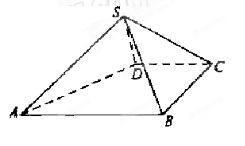
(12分) 22.已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,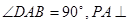
底面ABCD,PA=AD=DC=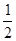 AB=1,M是PB的中点
AB=1,M是PB的中点
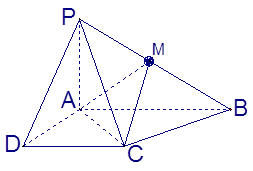
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求异面直线CM与AD所成角的正切值;
(Ⅲ)求面MAC与面BAC所成二面角的正切值
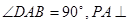
底面ABCD,PA=AD=DC=
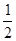 AB=1,M是PB的中点
AB=1,M是PB的中点
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求异面直线CM与AD所成角的正切值;
(Ⅲ)求面MAC与面BAC所成二面角的正切值
(1)略 (2)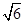 (3)
(3)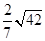
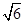 (3)
(3)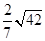
本题考查证明面面垂直的方法,求线线角即二面角的方法,关键是进行等价转化.
(1)先证明平面PAD⊥平面ABCD,再证得CD⊥平面PAD即可得到平面PAD⊥平面PCD.
(2)BP中点M,采用平移法得到异面直线的所成的角。
(3)根据三垂线定理可得二面角M-AC-B的平面角,解直角三角形求此角的大小.
(1)先证明平面PAD⊥平面ABCD,再证得CD⊥平面PAD即可得到平面PAD⊥平面PCD.
(2)BP中点M,采用平移法得到异面直线的所成的角。
(3)根据三垂线定理可得二面角M-AC-B的平面角,解直角三角形求此角的大小.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
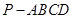 的底面
的底面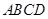 为矩形,且
为矩形,且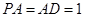 ,
,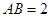 ,
, ,
,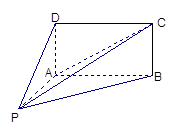
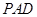 与平面
与平面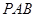 是否垂直?并说明理由;
是否垂直?并说明理由;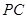 与平面
与平面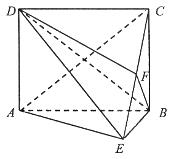
 中,
中,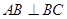 ,
,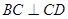 ,侧面
,侧面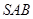 为等边三角形,
为等边三角形,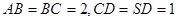 .
.
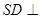 平面
平面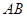 与平面
与平面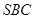 所成角的正弦值.
所成角的正弦值. 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.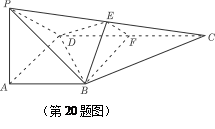
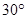 ,求k的取值范围.
,求k的取值范围.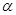 ∥平面
∥平面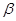 ,
,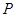 是
是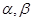 外一点,过点
外一点,过点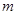 与
与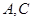 ,过点
,过点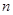 与
与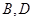 且
且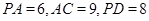 ,则
,则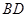 的长为
的长为 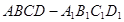 中,面对角线
中,面对角线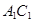 与体对角线
与体对角线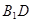 所成角等于
所成角等于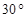
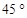
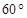
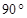
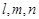 表示不同的直线,
表示不同的直线,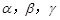 表示不同的平面,给出下列四个命题:
表示不同的平面,给出下列四个命题: 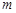 ∥
∥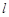 ,且
,且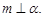 则
则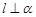 ;
; 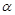 .则
.则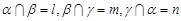 ,则
,则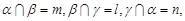 且n∥
且n∥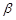 ,则
,则