题目内容
如图,已知△OFQ的面积为S,且![]() .
.
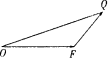
(1)若![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设|![]() |=c(c≥2),S=
|=c(c≥2),S=![]() ,若以O为中心,F为焦点的椭圆经过点Q,当|
,若以O为中心,F为焦点的椭圆经过点Q,当|![]() |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
答案:
解析:
解析:
|
解:(1)由已知,得 ∵ ∴2<tan (2)以O为原点, ∵△OFQ的面积为 又由 得x1= 当且仅当c=2时| 由此可得 故椭圆方程为 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

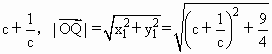 (c≥2).
(c≥2).
 如图,已知△OFQ的面积为S,且
如图,已知△OFQ的面积为S,且
 .
. ,求
,求 的范围;
的范围; 若以O为中心,F为一个焦点的椭圆经过点Q,以c为变量,当
若以O为中心,F为一个焦点的椭圆经过点Q,以c为变量,当 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.
 .
. ,求
,求 的范围;
的范围; 若以O为中心,F为一个焦点的椭圆经过点Q,以c为变量,当
若以O为中心,F为一个焦点的椭圆经过点Q,以c为变量,当 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.
 .
. ,求
,求 的范围;
的范围; 若以O为中心,F为一个焦点的椭圆经过点Q,以c为变量,当
若以O为中心,F为一个焦点的椭圆经过点Q,以c为变量,当 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.