题目内容
已知f(x)=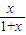 ,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1=
,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1= ,且bn+1=f(bn),
,且bn+1=f(bn),(1)求数列{an}和{bn}的通项公式
(2)令
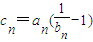 ,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.
,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.
【答案】分析:(1)由f(x)=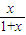 ,知f(1)=
,知f(1)= ,
,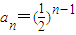 ,由b1=
,由b1= ,且bn+1=f(bn),得
,且bn+1=f(bn),得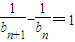 ,由此能求出数列{an}和{bn}的通项公式.
,由此能求出数列{an}和{bn}的通项公式.
(2)由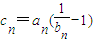 =n•
=n•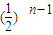 ,知
,知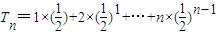 ,再由错位相减法能够求出结果.
,再由错位相减法能够求出结果.
解答:解:(1)∵f(x)=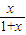 ,
,
∴f(1)=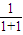 =
= ,
,
∵{an}为首项是1,以f(1)为公比的等比数列,
∴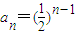 ,
,
∵b1= ,且bn+1=f(bn),
,且bn+1=f(bn),
∴bn+1=f(bn)=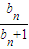 ,两边同时取倒数,
,两边同时取倒数,
得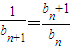 =1+
=1+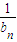 ,
,
∴ ,
,
∴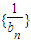 为等差数列,
为等差数列,
故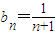 .
.
(2)∵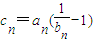 =n•
=n•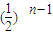 ,
,
∴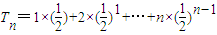 ,
,
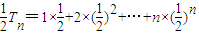 ,
,
两式相减整理,得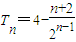 ,
,
∵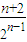 >0,
>0,
∴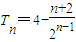 <4,
<4,
∵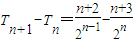
=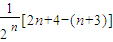
=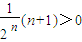 ,
,
∴{Tn}单调递增,
∴{Tn}min=T1=1,
所以1≤Tn<4.
点评:本试题主要考查等比数列和等差数列的通项公式的求解以及数列求和的综合运用.解决该试题的关键是整体构造等差数列法,以及错位相减法的准确运用.
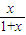 ,知f(1)=
,知f(1)= ,
,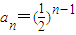 ,由b1=
,由b1= ,且bn+1=f(bn),得
,且bn+1=f(bn),得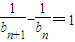 ,由此能求出数列{an}和{bn}的通项公式.
,由此能求出数列{an}和{bn}的通项公式.(2)由
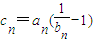 =n•
=n•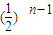 ,知
,知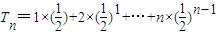 ,再由错位相减法能够求出结果.
,再由错位相减法能够求出结果.解答:解:(1)∵f(x)=
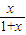 ,
,∴f(1)=
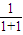 =
= ,
,∵{an}为首项是1,以f(1)为公比的等比数列,
∴
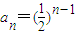 ,
,∵b1=
 ,且bn+1=f(bn),
,且bn+1=f(bn),∴bn+1=f(bn)=
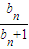 ,两边同时取倒数,
,两边同时取倒数,得
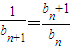 =1+
=1+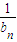 ,
,∴
 ,
,∴
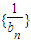 为等差数列,
为等差数列,故
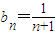 .
.(2)∵
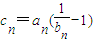 =n•
=n•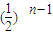 ,
,∴
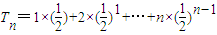 ,
,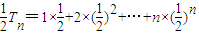 ,
,两式相减整理,得
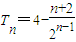 ,
,∵
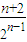 >0,
>0,∴
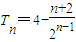 <4,
<4,∵
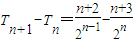
=
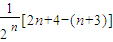
=
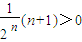 ,
,∴{Tn}单调递增,
∴{Tn}min=T1=1,
所以1≤Tn<4.
点评:本试题主要考查等比数列和等差数列的通项公式的求解以及数列求和的综合运用.解决该试题的关键是整体构造等差数列法,以及错位相减法的准确运用.

练习册系列答案
相关题目