题目内容
已知数列an是各项均不为0的等差数列,公差为d,Sn为其前n项和,且满足an2=S2n-1,n∈N*.数列bn满足 ,Tn为数列bn的前n项和.
,Tn为数列bn的前n项和.(1)求a1、d和Tn;
(2)若对任意的n∈N*,不等式λTn<n+8•(-1)n恒成立,求实数λ的取值范围;
(3)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
【答案】分析:(1)在an2=S2n-1中,令n=1,n=2,得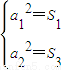 ,由此能求出求a1、d和Tn;
,由此能求出求a1、d和Tn;
(2)①当n为偶数时,要使不等式λTn<n+8•(-1)n恒成立,λ需满足λ<25.②当n为奇数时,要使不等式λTn<n+8•(-1)n恒成立,λ需满足λ<-21.综合①、②可得λ的取值范围.
(3)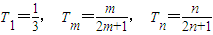 ,若T1,Tm,Tn成等比数列,则
,若T1,Tm,Tn成等比数列,则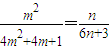 .由
.由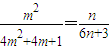 ,可得-2m2+4m+1>0,由此能求出求出所有m,n的值.
,可得-2m2+4m+1>0,由此能求出求出所有m,n的值.
解答:解:(1)在an2=S2n-1中,令n=1,n=2,
得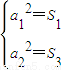 即
即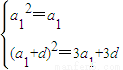 (2分)
(2分)
解得a1=1,d=2,(3分)∴an=2n-1.∵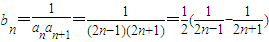 ,∴
,∴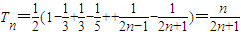 .(5分)
.(5分)
(2)①当n为偶数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式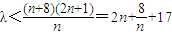 恒成立.(6分)∵
恒成立.(6分)∵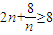 ,等号在n=2时取得.∴此时λ需满足λ<25.(7分)
,等号在n=2时取得.∴此时λ需满足λ<25.(7分)
②当n为奇数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式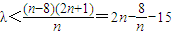 恒成立.(8分)∵
恒成立.(8分)∵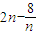 是随n的增大而增大,∴n=1时
是随n的增大而增大,∴n=1时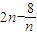 取得最小值-6.∴此时λ需满足λ<-21.(9分)
取得最小值-6.∴此时λ需满足λ<-21.(9分)
综合①、②可得λ的取值范围是λ<-21.(10分)
(3)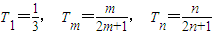 ,
,
若T1,Tm,Tn成等比数列,则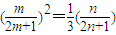 ,即
,即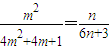 .(11分)
.(11分)
由 ,可得
,可得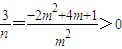 ,
,
即-2m2+4m+1>0,(12分)∴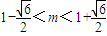 .(13分)
.(13分)
又m∈N,且m>1,所以m=2,此时n=12.
因此,当且仅当m=2,n=12时,数列 {Tn}中的T1,Tm,Tn成等比数列.(14分)
点评:本题考查了等差数列、等比数列的概念及其性质,以及数列的求和、利用均值不等式求最值等知识;考查了学生的函数思想方法,及其推理论证和探究的能力.
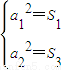 ,由此能求出求a1、d和Tn;
,由此能求出求a1、d和Tn;(2)①当n为偶数时,要使不等式λTn<n+8•(-1)n恒成立,λ需满足λ<25.②当n为奇数时,要使不等式λTn<n+8•(-1)n恒成立,λ需满足λ<-21.综合①、②可得λ的取值范围.
(3)
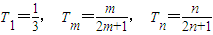 ,若T1,Tm,Tn成等比数列,则
,若T1,Tm,Tn成等比数列,则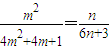 .由
.由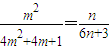 ,可得-2m2+4m+1>0,由此能求出求出所有m,n的值.
,可得-2m2+4m+1>0,由此能求出求出所有m,n的值.解答:解:(1)在an2=S2n-1中,令n=1,n=2,
得
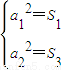 即
即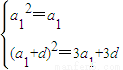 (2分)
(2分)解得a1=1,d=2,(3分)∴an=2n-1.∵
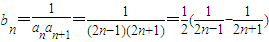 ,∴
,∴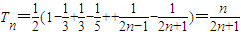 .(5分)
.(5分)(2)①当n为偶数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式
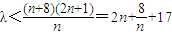 恒成立.(6分)∵
恒成立.(6分)∵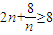 ,等号在n=2时取得.∴此时λ需满足λ<25.(7分)
,等号在n=2时取得.∴此时λ需满足λ<25.(7分)②当n为奇数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式
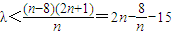 恒成立.(8分)∵
恒成立.(8分)∵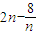 是随n的增大而增大,∴n=1时
是随n的增大而增大,∴n=1时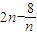 取得最小值-6.∴此时λ需满足λ<-21.(9分)
取得最小值-6.∴此时λ需满足λ<-21.(9分)综合①、②可得λ的取值范围是λ<-21.(10分)
(3)
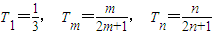 ,
,若T1,Tm,Tn成等比数列,则
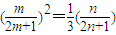 ,即
,即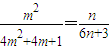 .(11分)
.(11分)由
 ,可得
,可得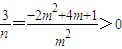 ,
,即-2m2+4m+1>0,(12分)∴
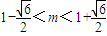 .(13分)
.(13分)又m∈N,且m>1,所以m=2,此时n=12.
因此,当且仅当m=2,n=12时,数列 {Tn}中的T1,Tm,Tn成等比数列.(14分)
点评:本题考查了等差数列、等比数列的概念及其性质,以及数列的求和、利用均值不等式求最值等知识;考查了学生的函数思想方法,及其推理论证和探究的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,Tn为数列bn的前n项和.
,Tn为数列bn的前n项和. ,Tn为数列bn的前n项和.
,Tn为数列bn的前n项和.