题目内容
8.若二次函数f(x)=ax2+bx+c(a≠0)满足f(x+2)-f(x)=x,且f(0)=1(Ⅰ)求f(x)的解析式;
(Ⅱ)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
分析 (Ⅰ)由待定系数法解方程组可得f(x)的解析式;
(Ⅱ)化恒成立为m小于函数y=$\frac{1}{4}$x2-$\frac{5}{2}$x+1在x∈[-1,1]的最小值,由二次函数区间的最值可得.
解答 解:(Ⅰ)∵二次函数f(x)=ax2+bx+c(a≠0)满足f(x+2)-f(x)=x,且f(0)=1,
∴f(0)=c=1,f(x+2)-f(x)=a(x+2)2+b(x+2)+1-ax2-bx-1=x,
整理可得(4a-1)x+4a+2b=0,∴4a-1=0且4a+2b=0,
解得a=$\frac{1}{4}$,b=$-\frac{1}{2}$,∴f(x)的解析式为f(x)=$\frac{1}{4}$x2-$\frac{1}{2}$x+1;
(Ⅱ)∵在区间[-1,1]上,不等式$\frac{1}{4}$x2-$\frac{1}{2}$x+1>2x+m恒成立,
∴在区间[-1,1]上m<$\frac{1}{4}$x2-$\frac{5}{2}$x+1恒成立,
只需m小于函数y=$\frac{1}{4}$x2-$\frac{5}{2}$x+1在x∈[-1,1]的最小值,
配方可得y=$\frac{1}{4}$(x-5)2-$\frac{21}{4}$,故当x=1时,y取最小值-$\frac{5}{4}$,
∴实数m的取值范围为m<-$\frac{5}{4}$.
点评 本题考查函数解析式求解的待定系数法,涉及恒成立和二次函数区间的最值,属中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
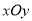 中,曲线
中,曲线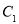 的参数方程为
的参数方程为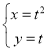 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,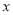 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线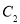 的极坐标方程为
的极坐标方程为 .
.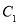 的参数方程化为极坐标方程 ;
的参数方程化为极坐标方程 ;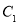 与
与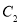 交点的极坐标(
交点的极坐标(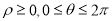 )
)