题目内容
(本题满分14分,其中第1小题6分,第2小题8分)
已知数列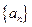 的首项为1,前
的首项为1,前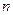 项和为
项和为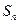 ,且满足
,且满足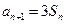 ,
,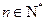 .数列
.数列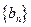 满足
满足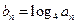 .
.
(1) 求数列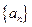 的通项公式;
的通项公式;
(2) 当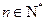 时,试比较
时,试比较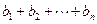 与
与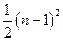 的大小,并说明理由.
的大小,并说明理由.
已知数列
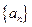 的首项为1,前
的首项为1,前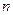 项和为
项和为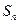 ,且满足
,且满足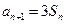 ,
,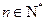 .数列
.数列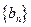 满足
满足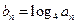 .
. (1) 求数列
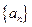 的通项公式;
的通项公式;(2) 当
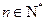 时,试比较
时,试比较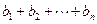 与
与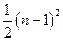 的大小,并说明理由.
的大小,并说明理由.略
略(1) 由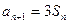 … (1) , 得 … (1) , 得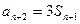 … (2),由 (2)-(1) 得 … (2),由 (2)-(1) 得 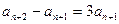 , 整理得 , 整理得 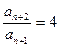 , ,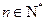 . .所以,数列 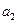 , ,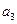 , ,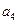 ,…, ,…,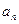 ,…是以4为公比的等比数列. ,…是以4为公比的等比数列.其中, 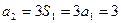 , ,所以, 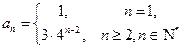 . . (2)由题意, 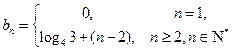 . .当 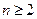 时, 时,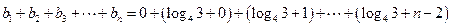 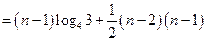 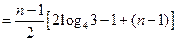 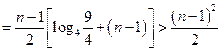 所以, 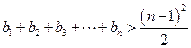 . . |
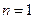 时,
时,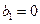 ,
,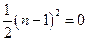 .
.故综上,当
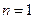 时,
时,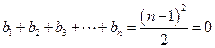 ;
;当
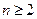 时,
时,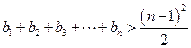 .
.
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
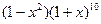 原式展开式中,
原式展开式中,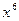 项的系数是___________.
项的系数是___________.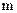 接力赛跑。第一棒只能从甲、乙两人中安排1人,第四棒只能从甲、丙两人中安排1人,则不同的安排方案共有
接力赛跑。第一棒只能从甲、乙两人中安排1人,第四棒只能从甲、丙两人中安排1人,则不同的安排方案共有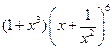 展开式中的常数项为 .
展开式中的常数项为 . 为1、2、3、4四个盒子中,依下列条件各有多少种放法。
为1、2、3、4四个盒子中,依下列条件各有多少种放法。