题目内容
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.(1)若AE=CD,点M为BC的中点,求证:直线MP∥平面EAB
(2)若AE=2,CD=1,求锐二面角E-BC-A的平面角的余弦值.

【答案】分析:(1)由题意可得四边形ACDE为矩形,点P为EC的中点.再取AC的中点为N,可证MN∥平面EAB,PN∥平面EAB,从而平面PMN∥平面EAB.再根据两个平面平行的性质可得直线MP∥平面EAB.
(2)先由条件判断∠EBA即为锐二面角E-BC-A的平面角.直角三角形EAB中,由EA=AB=2,可得直角三角形EAB为等腰直角三角形,故∠EBA=45°,由此求得cos∠EBA 的值,即为所求.
解答: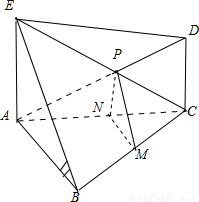 解:(1)∵AE=CD,点M为BC的中点,AE⊥平面ABC,CD⊥平面ABC,故四边形ACDE为矩形.
解:(1)∵AE=CD,点M为BC的中点,AE⊥平面ABC,CD⊥平面ABC,故四边形ACDE为矩形.
由CE交AD于点,P可得点P为EC的中点.
再取AC的中点为N,则MN为△ABC的中位线,PN为△ACE的中位线,故有MN∥AB,
而MN不在平面ABE中,AB在平面ANE中,故有MN∥平面EAB.
同理可证,PN∥平面EAB.
而MN和PN是平面PMN内的两条相交直线,故平面PMN∥平面EAB.
而MP在平面PMN内,故MP∥平面EAB.
(2)Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,则有BC⊥平面EAB,
故∠EBA即为锐二面角E-BC-A的平面角.
直角三角形EAB中,由EA=AB=2,可得直角三角形EAB为等腰直角三角形,
故∠EBA=45°,∴cos∠EBA= .
.
点评:本题主要考查证明直线和平面平行、2个平面平行的方法,2个平面平行的性质,求二面角的平面角,属于中档题.
(2)先由条件判断∠EBA即为锐二面角E-BC-A的平面角.直角三角形EAB中,由EA=AB=2,可得直角三角形EAB为等腰直角三角形,故∠EBA=45°,由此求得cos∠EBA 的值,即为所求.
解答:
 解:(1)∵AE=CD,点M为BC的中点,AE⊥平面ABC,CD⊥平面ABC,故四边形ACDE为矩形.
解:(1)∵AE=CD,点M为BC的中点,AE⊥平面ABC,CD⊥平面ABC,故四边形ACDE为矩形.由CE交AD于点,P可得点P为EC的中点.
再取AC的中点为N,则MN为△ABC的中位线,PN为△ACE的中位线,故有MN∥AB,
而MN不在平面ABE中,AB在平面ANE中,故有MN∥平面EAB.
同理可证,PN∥平面EAB.
而MN和PN是平面PMN内的两条相交直线,故平面PMN∥平面EAB.
而MP在平面PMN内,故MP∥平面EAB.
(2)Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,则有BC⊥平面EAB,
故∠EBA即为锐二面角E-BC-A的平面角.
直角三角形EAB中,由EA=AB=2,可得直角三角形EAB为等腰直角三角形,
故∠EBA=45°,∴cos∠EBA=
 .
.点评:本题主要考查证明直线和平面平行、2个平面平行的方法,2个平面平行的性质,求二面角的平面角,属于中档题.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=