��Ŀ����
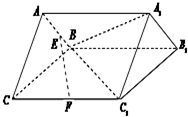 ��ͼ��������ABC-A1B1C1�У�BC=2��BC1=
��ͼ��������ABC-A1B1C1�У�BC=2��BC1=| 2 |
| 2 |
�������߶�CC1���Ƿ����һ��F��ʹ��EF��ƽ��A1BC1�������ڣ�ȷ����λ�ã��������ڣ�˵�����ɣ�
�������߶�CC1���Ƿ����һ��F��ʹ��EF��BB1�������ڣ�ȷ����λ�ã��������ڣ�˵�����ɣ�
�� III����FΪCC1���е�ʱ����AC��CC1����EF��ƽ��ACC1A1���ɵĽǵ�����ֵΪ
| ||
| 3 |
��������I�����ڣ��е㣬��������ƽ�е��ж������ɵý��ۣ�
�����ڣ���F�ڿ��˵�C1һ����ĵȷֵ�ʱ��
��III�������ռ�ֱ������ϵ��ȷ��ƽ��ACC1A1��ƽ��AA1B��һ�������������������ļнǹ�ʽ�����ɵõ����ۣ�
�����ڣ���F�ڿ��˵�C1һ����ĵȷֵ�ʱ��
��III�������ռ�ֱ������ϵ��ȷ��ƽ��ACC1A1��ƽ��AA1B��һ�������������������ļнǹ�ʽ�����ɵõ����ۣ�
����⣺ ��I�����ڣ��е㣮
��I�����ڣ��е㣮
ȡA1B���е�D������ED��DC1����ED��AA1��ED=
AA1��
��FΪCC1�ϵĶ��㣬��ED��FC1��ED=FC1��
���ı���DEFC1��ƽ���ı���
��EF��DC1��
��EF?ƽ��A1BC1��DC1?ƽ��A1BC1��
��EF��ƽ��A1BC1��
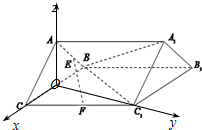
�����ڣ���F�ڿ��˵�C1һ����ĵȷֵ�ʱ��������ͼ��ʾ�Ŀռ�ֱ������ϵ����A��0��0��b����F��x��1-x��0������E��-
��0��
������
=(x+
��1-x��
)����
=(-1��1��0)��
��
����x=
��
��III����ƽ��ACC1A1��һ��������Ϊ
1=(x1��y1��z1)
��
=(-1��1��0)��
=(1��0��-b)
��
��
����z1=1����
1=(b��b��1)
��
=(1��
��-
)
��|cos��
��
��|=
=
=
����6�֣�
���b=1����b=
��
��AC��CC1��b=1
��
1=(1��1��1)
ͬ�������ƽ��AA1B��һ��������
=(1��1��-1)
��cos��
��
��=
=
�ֶ����C-AA1-BΪ�����ǣ�������ֵΪ
��
 ��I�����ڣ��е㣮
��I�����ڣ��е㣮ȡA1B���е�D������ED��DC1����ED��AA1��ED=
| 1 |
| 2 |
��FΪCC1�ϵĶ��㣬��ED��FC1��ED=FC1��
���ı���DEFC1��ƽ���ı���
��EF��DC1��
��EF?ƽ��A1BC1��DC1?ƽ��A1BC1��
��EF��ƽ��A1BC1��
�����ڣ���F�ڿ��˵�C1һ����ĵȷֵ�ʱ��������ͼ��ʾ�Ŀռ�ֱ������ϵ����A��0��0��b����F��x��1-x��0������E��-
| 1 |
| 2 |
| b |
| 2 |
| EF |
| 1 |
| 2 |
| b |
| 2 |
| CC1 |
| EF |
| CC1 |
| 1 |
| 4 |
��III����ƽ��ACC1A1��һ��������Ϊ
| n |
��
| CC1 |
| AC |
��
|
|
| n |
��
| EF |
| 1 |
| 2 |
| b |
| 2 |
��|cos��
| n1 |
| EF |
|
| ||||
|
|
| b | ||||||||
|
| ||
| 3 |
���b=1����b=
| ||
| 2 |
��AC��CC1��b=1
��
| n |
ͬ�������ƽ��AA1B��һ��������
| n2 |
��cos��
| n1 |
| n2 |
| ||||
|
|
| 1 |
| 3 |
�ֶ����C-AA1-BΪ�����ǣ�������ֵΪ
| 1 |
| 3 |
���������⿼������ƽ�У���������ǣ���������֪ʶ�����ã�����ѧ�������������������������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

 ��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC��AB��AC��D��E�ֱ�ΪAA1��B1C���е㣬AB=AC��
��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC��AB��AC��D��E�ֱ�ΪAA1��B1C���е㣬AB=AC�� ��2012•����������ͼ��������ABC-A1B1C1�У����ⴹֱ���棬��ACB=90�㣬AC=BC=
��2012•����������ͼ��������ABC-A1B1C1�У����ⴹֱ���棬��ACB=90�㣬AC=BC= ��ͼ��������ABC-A1B1C1�ĵ���ABCΪ�������Σ�����AA1��ƽ��ABC��D��BC�е㣬��AA1=AB
��ͼ��������ABC-A1B1C1�ĵ���ABCΪ�������Σ�����AA1��ƽ��ABC��D��BC�е㣬��AA1=AB ��2012•������ģ����ͼ��������ABC-A��B��C�䣬cc��=
��2012•������ģ����ͼ��������ABC-A��B��C�䣬cc��=