题目内容
 一个三棱锥的棱长均为2,四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(三棱锥的截面)的面积是( )
一个三棱锥的棱长均为2,四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(三棱锥的截面)的面积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据球内接正四面体的性质与圆的对称性,可得图中的截面是三棱锥的一条棱与高线所在的平面,即这条棱和与其相对棱的中点构成的三角形.由此作出图形并利用题中的数据加以计算,可得此截面的面积.
解答:解: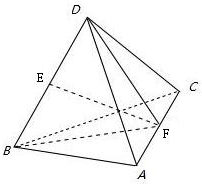 根据题意,过该球球心的一个截面经过三棱锥的一条棱,且截面为等腰三角形.
根据题意,过该球球心的一个截面经过三棱锥的一条棱,且截面为等腰三角形.
因此该截面所在平面与球相交截得球大圆,即球心在此截面内,
由球的对称性可得球心在该三棱锥的高上,
∴该截面是三棱锥的一条棱与高线所在的平面,即这条棱和与其相对棱的中点构成的三角形,
因此设三棱锥D-ABC中,截面三角形为△BDF,其中F为棱AC的中点
∵三棱锥的棱长均为2,∴DF=DF=
×2=
.
取BD的中点E,连结EF,则EF是等腰△BDF底边上的高,
∵EF=
=
,
∴△BDF的面积为S=
BD•EF=
×2×
=
.
故选:C
 根据题意,过该球球心的一个截面经过三棱锥的一条棱,且截面为等腰三角形.
根据题意,过该球球心的一个截面经过三棱锥的一条棱,且截面为等腰三角形.因此该截面所在平面与球相交截得球大圆,即球心在此截面内,
由球的对称性可得球心在该三棱锥的高上,
∴该截面是三棱锥的一条棱与高线所在的平面,即这条棱和与其相对棱的中点构成的三角形,
因此设三棱锥D-ABC中,截面三角形为△BDF,其中F为棱AC的中点
∵三棱锥的棱长均为2,∴DF=DF=
| ||
| 2 |
| 3 |
取BD的中点E,连结EF,则EF是等腰△BDF底边上的高,
∵EF=
| BF2-BE2 |
| 2 |
∴△BDF的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故选:C
点评:本题给出球内接正四面体的一个截面的形状,求该截面的面积.着重考查了正四面体的性质、圆的对称性、勾股定理与三角形的面积计算等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个三棱锥铁框架的棱长均为2,其内置一气球,使其充气至尽可能的膨胀(保持球的形状),则此球的表面积为( )
A、
| ||
| B、2π | ||
| C、3π | ||
| D、6π |