题目内容
 已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y
已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y(1)求以A、B为焦点,且过C、D两点的椭圆C的标准方程;
(2)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,
| |0P| | |0M| |
分析:(1)由椭圆的定义可得2c=AB可求c,在长方形ABCD,由AB=6,BC=
可得AC,根据椭圆的定义可得,2a=CA+CB可求a,进而可求b及椭圆的方程
(2)设M(x,y),其中x∈[-4,4].由已知
=λ,及点P在椭圆C上可得((16λ2-9)x2+16λ2y2=112,x∈[-4,4],根据方程的特点,故讨论二次项系数16λ2-9=0,16λ2-9>0,16λ2-9<0三种情况讨论,从而可得方程代表的曲线类型
| 7 |
| 4 |
(2)设M(x,y),其中x∈[-4,4].由已知
| |0P| |
| |0M| |
解答:解:(1)由椭圆的定义可得2c=AB=6,c=3
在长方形ABCD,由AB=6,BC=
可得AC=
=
,
∴2a=CA+CB=8,a=4∴b2=a2-c2=7
椭圆的方程为
+
=1…(5分)
(2)设M(x,y),其中x∈[-4,4].由已知
=λ,及点P在椭圆C上可得
=λ2.整理得((16λ2-9)x2+16λ2y2=112,x∈[-4,4]…(8分)
(i)λ=
时.化简得9y2=112
所以点M的轨迹方程为y=±
(-4≤x≤4),轨迹是两条平行于x轴的线段.
(ii)λ≠
时,方程变形为
+
=1,其中x∈[-4,4]
当0<λ<
时,点M的轨迹为中心在原点、实轴在y轴上的双曲线满足-4≤x≤4的部分.
当
<λ<1时,点M的轨迹为中心在原点、长轴在x轴上的椭圆满足-4≤x≤4的部分;
当λ≥1时,点M的轨迹为中心在原点、长轴在x轴上的椭圆…(13分)
在长方形ABCD,由AB=6,BC=
| 7 |
| 4 |
36+
|
| 25 |
| 4 |
∴2a=CA+CB=8,a=4∴b2=a2-c2=7
椭圆的方程为
| x2 |
| 16 |
| y2 |
| 7 |
(2)设M(x,y),其中x∈[-4,4].由已知
| |0P| |
| |0M| |
| 9x2+112 |
| 16(x2+y2) |
(i)λ=
| 3 |
| 4 |
所以点M的轨迹方程为y=±
4
| ||
| 3 |
(ii)λ≠
| 3 |
| 4 |
| x2 | ||
|
| y2 | ||
|
当0<λ<
| 3 |
| 4 |
当
| 3 |
| 4 |
当λ≥1时,点M的轨迹为中心在原点、长轴在x轴上的椭圆…(13分)
点评:本题主要考查了利用椭圆的定义求解椭圆的参数a,c,b的值,进而求解椭圆的方程,及二次曲线表示椭圆、双曲线、圆的条件的考查.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 如图,已知长方形ABCD的两条对角线的交点为E(1,0),且AB与BC所在的直线方程分别为:x+3y-5=0与ax-y+5=0.
如图,已知长方形ABCD的两条对角线的交点为E(1,0),且AB与BC所在的直线方程分别为:x+3y-5=0与ax-y+5=0.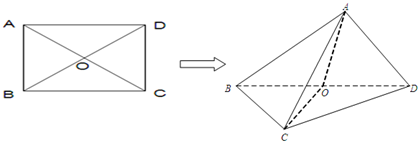
 (2013•日照一模)已知长方形ABCD,AB=2
(2013•日照一模)已知长方形ABCD,AB=2