题目内容
已知点 ,
, ,动点
,动点 的轨迹曲线
的轨迹曲线 满足
满足 ,
, ,过点
,过点 的直线交曲线
的直线交曲线 于
于 、
、 两点.
两点.
(1)求 的值,并写出曲线
的值,并写出曲线 的方程;
的方程;
(2)求△ 面积的最大值.
面积的最大值.
 ,
, ,动点
,动点 的轨迹曲线
的轨迹曲线 满足
满足 ,
, ,过点
,过点 的直线交曲线
的直线交曲线 于
于 、
、 两点.
两点.(1)求
 的值,并写出曲线
的值,并写出曲线 的方程;
的方程;(2)求△
 面积的最大值.
面积的最大值.(1)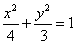
(2)△ 面积的最大值为3,此时直线
面积的最大值为3,此时直线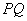 的方程为
的方程为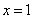 .
.
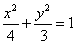
(2)△
 面积的最大值为3,此时直线
面积的最大值为3,此时直线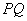 的方程为
的方程为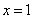 .
. 试题分析:解:(1)设
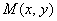 ,在△
,在△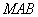 中,
中,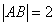 ,
, ,根据余弦定理得
,根据余弦定理得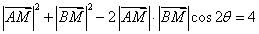 . (2分)
. (2分)即
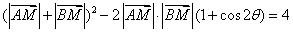 .
.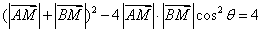 .
.而
 ,所以
,所以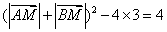 .
. 所以
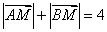 . (4分)
. (4分) 又
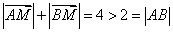 ,
,因此点
 的轨迹是以
的轨迹是以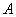 、
、 为焦点的椭圆(点
为焦点的椭圆(点 在
在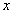 轴上也符合题意),
轴上也符合题意),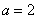 ,
,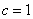 .
.所以曲线
 的方程为
的方程为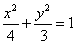 . (6分)
. (6分)(2)设直线
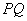 的方程为
的方程为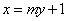 .
.由
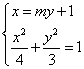 ,消去x并整理得
,消去x并整理得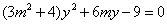 . ①
. ①显然方程①的
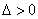 ,设
,设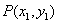 ,
,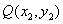 ,则
,则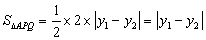
由韦达定理得
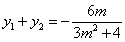 ,
,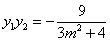 . (9分)
. (9分)所以
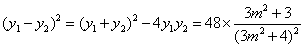 .
.令
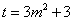 ,则
,则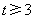 ,
,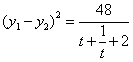 .
.由于函数
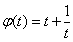 在
在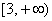 上是增函数.
上是增函数.所以
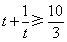 ,当
,当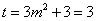 ,即
,即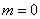 时取等号.
时取等号.所以
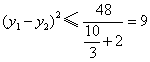 ,即
,即 的最大值为3.
的最大值为3.所以△
 面积的最大值为3,此时直线
面积的最大值为3,此时直线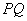 的方程为
的方程为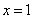 . (12分)
. (12分)点评:解决的关键是根据椭圆的定义求解轨迹方程,同时结合直线与椭圆方程来联立方程组来求解最值,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是平面上一点,
是平面上一点, 是平面上不共线三点,动点
是平面上不共线三点,动点 满足:
满足:
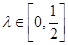 ,已知
,已知 时,
时, .则
.则 的最小值____________.
的最小值____________.
 ,
,
 ,且
,且 ,则
,则 的值为 .
的值为 . 为抛物线
为抛物线 的焦点,
的焦点, 、
、 、
、 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则 ( )
( )  ,
,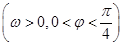 ,函数
,函数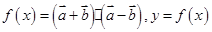 图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点
图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点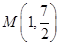 。
。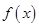 的解析式
的解析式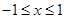 时,求函数
时,求函数 ,向量
,向量 ,则A
,则A
 ( )
( )



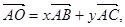 x+2y=1,则
x+2y=1,则 ;
;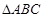 所在平面内一点,且满足
所在平面内一点,且满足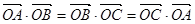 ,则点O是
,则点O是 ,
, ,且
,且 ,则锐角
,则锐角 为________.
为________.