题目内容
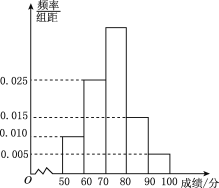
【题目】从2013年开始,国家教育部要求高中阶段每学年都要组织学生进行学生体质健康测试,方案要求以学校为单位组织实施,某校对高一(1)班学生根据《国家学生体质健康标准》的测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图.所示,已知[90,100]分数段的人数为2.
(1)求[70,80)分数段的人数;
(2)现根据预备测试成绩从成绩在80分以上(含80分)的学生中任意选出2人代表班级参加学校举行的一项体育比赛,求这2人的成绩一个在[80,90)分数段、一个在[90,100]分数段的概率.
【答案】(1)18;(2)![]()
【解析】
⑴由频率分布直方图可知,各个分数段的频率,求出![]() 分以上的总人数,
分以上的总人数,![]() 分数段的频率,即可求出人数
分数段的频率,即可求出人数
⑵求得![]() 分数段的人数,列举出所有可能性情况,然后计算结果
分数段的人数,列举出所有可能性情况,然后计算结果
(1)由频率分布直方图可知,[90,100]分数段的频率为0.005×10=0.05,
[70,80)分数段的频率为1-(0.010+0.025+0.015+0.005)×10=0.45,
因为[90,100]分数段的人数为2,所以50分以上的总人数为![]() =40,
=40,
所以[70,80)分数段的人数为40×0.45=18.
(2)由(1)可求得[80,90)分数段的人数为40×0.15=6,
设[80,90)分数段的6名学生分别为A1,A2,A3,A4,A5,A6,[90,100]分数段的2名学生分别为B1,B2,
则从中选出2人的选法有(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A2,B1),(A2,B2),(A3,A4),(A3,A5),(A3,A6),(A3,B1),(A3,B2),(A4,A5),(A4,A6),(A4,B1),(A4,B2),(A5,A6),(A5,B1),(A5,B2),(A6,B1),(A6,B2),(B1,B2),共28种.
其中这2人的成绩一个在[80,90)分数段、一个在[90,100]分数段的情况有(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(A5,B1),(A5,B2),(A6,B1),(A6,B2),共12种,
则所求概率P=![]() =
=![]() .
.

【题目】受电视机在保修期内维修费等因素的影响,企业生产每台电视机的利润与该电视机首次出现故障的时间有关.某电视机制造厂生产甲、乙两种型号电视机,保修期均为2年,现从该厂已售出的两种型号电视机中各随机抽取50台,统计数据如下:
品牌 | 甲 | 乙 | |||
首次出现故障时间x(年) |
|
|
|
|
|
电视机数量(台) | 3 | 5 | 42 | 8 | 42 |
每台利润(千元) | 1 | 2 | 3 | 1.8 | 2.8 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲种型号电视机中随机抽取一台,求首次出现故障发生在保修期内的概率;
(2)该厂预计今后这两种型号电视机销量相当,由于资金限制,只能生产其中一种型号电视机,若从经济效益的角度考虑,你认为应该产生哪种型号电视机?说明理由.
【题目】某企业生产一种产品,从流水线上随机抽取![]() 件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在
件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损
的为特优品,销售时劣质品每件亏损![]() 元,优等品每件盈利
元,优等品每件盈利![]() 元,特优品每件盈利
元,特优品每件盈利![]() 元,以这
元,以这![]() 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
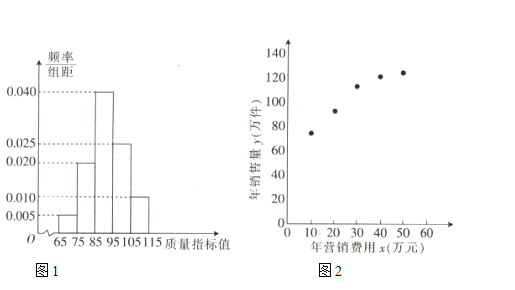
(1)求每件产品的平均销售利润;
(2)该企业主管部门为了解企业年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对该企业近
(单位:万件)的影响,对该企业近![]() 年的年营销费用
年的年营销费用![]() 和年销售量
和年销售量![]() ,
,![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
②用所求的回归方程估计该企业每年应投入多少营销费,才能使得该企业的年收益的预报值达到最大?(收益![]() 销售利润
销售利润![]() 营销费用,取
营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为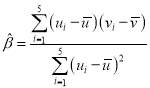 ,
,![]() .
.
【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:

注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?