题目内容
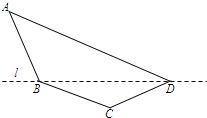 (2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
(2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.(1)设AB=x米,cosA=f(x),求f(x)的解析式,并指出x的取值范围;
(2)求四边形ABCD面积的最大值.
分析:(1)在△ABD与△CBD中,分别利用余弦定理,即可确定f(x)的解析式,及x的取值范围;
(2)四边形ABCD的面积S=
(AB•AD+CB•CD)sinA=
,构建函数g(x)=(x2-4)( x2-14x+49),x∈(2,5),求导函数,即可求得四边形ABCD面积的最大值.
(2)四边形ABCD的面积S=
| 1 |
| 2 |
| (x2-4)(x2-14x+49) |
解答:解:(1)设AB=x米,则BC=x米,CD=5-x米,AD=9-x米,
则有5-x>0,即x<5.
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB•AD•cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC. …(3分)
因为∠A和∠C互补,所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA. …(5分)
即x2+(9-x)2-2 x(9-x)cosA=x2+(5-x)2+2 x(5-x)cosA.
解得cosA=
,即f(x)=
.
由余弦的定义,有
<1,则x>2,
故x∈(2,5). …(8分)
(2)四边形ABCD的面积S=
(AB•AD+CB•CD)sinA=
[x(5-x)+x(9-x)]
=
.…(11分)
记g(x)=(x2-4)(x2-14x+49),x∈(2,5).
由g′(x)=2x(x2-14x+49)+(x2-4)(2 x-14)=2(x-7)(2 x2-7 x-4)=0,
∴x=4或x=7或x=-
.
∵x∈(2,5),∴x=4. …(14分)
所以函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.
因此g(x)的最大值为g(4)=12×9=108.
所以S的最大值为
=6
.
答:所求四边形ABCD面积的最大值为6
m2. …(16分)
则有5-x>0,即x<5.
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB•AD•cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC. …(3分)
因为∠A和∠C互补,所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA. …(5分)
即x2+(9-x)2-2 x(9-x)cosA=x2+(5-x)2+2 x(5-x)cosA.
解得cosA=
| 2 |
| x |
| 2 |
| x |
由余弦的定义,有
| 2 |
| x |
故x∈(2,5). …(8分)
(2)四边形ABCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2A |
| (x2-4)(x2-14x+49) |
记g(x)=(x2-4)(x2-14x+49),x∈(2,5).
由g′(x)=2x(x2-14x+49)+(x2-4)(2 x-14)=2(x-7)(2 x2-7 x-4)=0,
∴x=4或x=7或x=-
| 1 |
| 2 |
∵x∈(2,5),∴x=4. …(14分)
所以函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.
因此g(x)的最大值为g(4)=12×9=108.
所以S的最大值为
| 108 |
| 3 |
答:所求四边形ABCD面积的最大值为6
| 3 |
点评:本题考查函数解析式,考查余弦定理的运用,考查四边形面积的计算,考查利用导数求函数的最值,正确表示四边形的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为
(2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为