题目内容
在△ABC中,已知a=5,b=4,cos(A-B)=| 31 | 32 |
分析:先作∠BAD=B交边BC于点D,根据余弦定理求出AD的长度,再根据等腰三角形的性质可得到CD的长度,最后根据余弦定理求出角C的余弦值,进而得到角C的值.
解答: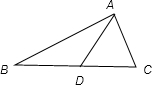 解:∵a>b,∴A>B.
解:∵a>b,∴A>B.
作∠BAD=B交边BC于点D.
设BD=x,则AD=x,DC=5-x.
在△ADC中,cos∠DAC=cos(A-B)=
,由余弦定理得:
(5-x)2=x2+42-2x•4•
,
即:25-10x=16-
,
解得:x=4.
∴在△ADC中,AD=AC=4,CD=1,
由余弦定理可得 cosC=
=
=
∴C=arccos
 解:∵a>b,∴A>B.
解:∵a>b,∴A>B.作∠BAD=B交边BC于点D.
设BD=x,则AD=x,DC=5-x.
在△ADC中,cos∠DAC=cos(A-B)=
| 31 |
| 32 |
(5-x)2=x2+42-2x•4•
| 31 |
| 32 |
即:25-10x=16-
| 31x |
| 4 |
解得:x=4.
∴在△ADC中,AD=AC=4,CD=1,
由余弦定理可得 cosC=
| CD2+AC2-AD2 |
| 2×CD×AC |
| 1+16-16 |
| 2×1×4 |
| 1 |
| 8 |
∴C=arccos
| 1 |
| 8 |
点评:本题主要考查余弦定理的应用.关键在于能够勾画出角A-B的值,再运用余弦定理即可解题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目