Question

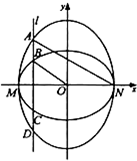如图，已知MN分别是椭圆C₁、C₂的长轴和短轴，且C₁、C₂的离心率都等于

2

2

，直线l⊥MN，l与C₁交于B，C两点，与C₂交于A，D两点．
（I）当|MN|=4时，求C₁，C₂的方程；
（II）当l平行移动时，
（ⅰ）证明：|BC|：|AD|为定值；
（ⅱ）是否存在直线l，使BO∥AN？若存在，求直线l的方程；若不存在，请说明理由．
（ⅱ）是否存在直线l，使BO∥AN？若存在，求直线l的方程；若不存在，请说明理由．

Answer 1

分析：（I）根据MN分别是椭圆C₁、C₂的长轴和短轴，且C₁、C₂的离心率都等于

2

2

，确定几何量之间的关系，即可求得椭圆的方程；
（II）（ⅰ）根据C₁、C₂的离心率都等于

2

2

，可设C₁，C₂的方程，设l：x=t（|t|＜a），分别与C₁、C₂方程联立，求得A，B的坐标，即可证得结论；（ⅱ）t=0时的l不符合题意；t≠0时，BO∥AN?k_BO=k_AN，利用BO∥AN建立等式，求得t=-a，与|t|＜a矛盾，故可得结论．

解答：（I）解：∵C₁离心率都等于

2

2

，长轴长|MN|=4，
∴a=2，

c

a

=

2

2

∴c=

2

∴b²=a²-c²=2
∴C₁方程为

x2

4

+

y2

2

=1；
∵C₂的离心率都等于

2

2

，短轴长|MN|=4，
∴C₂方程为

x2

4

+

y2

8

=1；
（II）（ⅰ）证明：由于C₁、C₂的离心率都等于

2

2

，可设C₁：

x2

a2

+

2y2

a2

=1，C₂：

x2

a2

+

y2

2a2

=1
设l：x=t（|t|＜a），分别与C₁、C₂方程联立，求得A（t，

2(a2-t2)

），B（t，

2(a2-t2)

2

）
∴|BC|：|AD|=

1

2

为定值；
（ⅱ）解：t=0时的l不符合题意．…（9分）
t≠0时，BO∥AN?k_BO=k_AN
而kOB=

2(a2-t2)

2t

，kAN=

2(a2-t2)

t-a

所以BO∥AN?

2(a2-t2)

2t

=

2(a2-t2)

t-a

…（11分）
解得t=-a，与|t|＜a矛盾，所以不存在直线l，使BO∥AN．…（12分）

点评：本题考查椭圆的标准方程，考查椭圆的几何性质，考查直线与椭圆的位置关系，属于中档题．