题目内容
如图,在棱长为2的正方体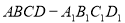 内(含正方体表面)任取一点
内(含正方体表面)任取一点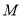 ,则
,则 的概率
的概率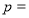 .
.
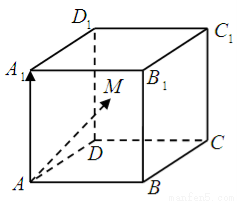
【解析】
试题分析:以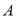 为原点
为原点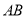 为
为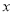 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则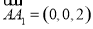 ,设
,设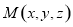 ,则
,则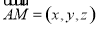 ,则
,则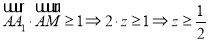 ,从而
,从而 .
.
考点:1.空间向量的数量积;2.几何概型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,在棱长为2的正方体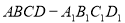 内(含正方体表面)任取一点
内(含正方体表面)任取一点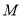 ,则
,则 的概率
的概率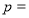 .
.

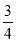
【解析】
试题分析:以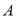 为原点
为原点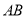 为
为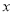 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则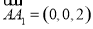 ,设
,设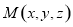 ,则
,则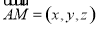 ,则
,则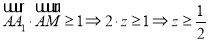 ,从而
,从而 .
.
考点:1.空间向量的数量积;2.几何概型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案