题目内容
将一颗骰子先后抛掷两次,得到的点数分别记为 ,
, 则直线
则直线 与圆
与圆 不相切的概率为
不相切的概率为
 ,
, 则直线
则直线 与圆
与圆 不相切的概率为
不相切的概率为A. | B. | C. | D. |
B
此题考查古典概型概率的计算
思路分析:先列出所有的基本事件,然后确定直线 与圆
与圆 相切的所包含的事件个数,再确定直线
相切的所包含的事件个数,再确定直线 与圆
与圆 不相切的所包含的事件个数,然后根据古典概型概率计算公式计算
不相切的所包含的事件个数,然后根据古典概型概率计算公式计算
解:所有的可能结果有:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),(2,3),(2,4),(2,5),(2,6),(3,3),(3,4),(3,5),(3,6),(4,4),(4,5),(4,6),(5,5),(5,6),(6,6), (2,1),(3,1),(4,1),(5,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),( 5,3),( 6,3), (5,4),( 6,4), (6,5).共36种结果,若直线 与圆
与圆 相切,则
相切,则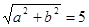 ,有(3,4),(4,3)两个,那么满足直线
,有(3,4),(4,3)两个,那么满足直线 与圆
与圆 不相切有36-2=34即所求事件包含34个基本事件,由古典概型的概率计算公式得
不相切有36-2=34即所求事件包含34个基本事件,由古典概型的概率计算公式得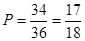 .选B.
.选B.
答案:B.
点评:解答此题需考虑所求事件的对立事件.
思路分析:先列出所有的基本事件,然后确定直线
 与圆
与圆 相切的所包含的事件个数,再确定直线
相切的所包含的事件个数,再确定直线 与圆
与圆 不相切的所包含的事件个数,然后根据古典概型概率计算公式计算
不相切的所包含的事件个数,然后根据古典概型概率计算公式计算解:所有的可能结果有:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),(2,3),(2,4),(2,5),(2,6),(3,3),(3,4),(3,5),(3,6),(4,4),(4,5),(4,6),(5,5),(5,6),(6,6), (2,1),(3,1),(4,1),(5,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),( 5,3),( 6,3), (5,4),( 6,4), (6,5).共36种结果,若直线
 与圆
与圆 相切,则
相切,则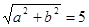 ,有(3,4),(4,3)两个,那么满足直线
,有(3,4),(4,3)两个,那么满足直线 与圆
与圆 不相切有36-2=34即所求事件包含34个基本事件,由古典概型的概率计算公式得
不相切有36-2=34即所求事件包含34个基本事件,由古典概型的概率计算公式得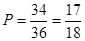 .选B.
.选B.答案:B.
点评:解答此题需考虑所求事件的对立事件.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
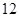 只,其中有
只,其中有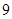 只合格品,
只合格品,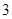 只次品.
只次品.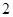 次取到次品”的概率;
次取到次品”的概率;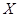 ”的分布列和数学期望.
”的分布列和数学期望. (必然事件)=100
(必然事件)=100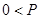 (不确定事件)
(不确定事件)
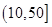
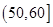
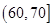
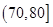
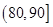
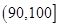
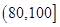 内的频率为 。
内的频率为 。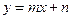 .设集合
.设集合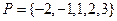 和
和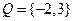 ,分别从集合
,分别从集合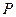 和
和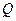 中随机取一个数作为
中随机取一个数作为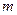 和
和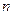 ,则函数
,则函数