题目内容
如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE方便花园管理.设D、E分别在AB、AC上,且DE均分三角形ABC的面积.
(1)设AD=x(x≥a),DE=y,试将y表示为x的函数关系式;
(2)若DE是灌溉水管,为节约成本,希望其最短,DE的位置应在哪里?若DE是参观路线,希望其最长,DE的位置应在哪里?

(1)设AD=x(x≥a),DE=y,试将y表示为x的函数关系式;
(2)若DE是灌溉水管,为节约成本,希望其最短,DE的位置应在哪里?若DE是参观路线,希望其最长,DE的位置应在哪里?

(1)因为DE均分三角形ABC的面积,
所以xAE=
(2a)2,即AE=
.
在△ADE中,由余弦定理得y=
.
因为0≤AD≤2a,0≤AE≤2a,所以
解得a≤x≤2a.
故y关于x的函数关系式为y=
(a≤x≤2a).
(2)令t=x2,则a2≤t≤2a2,且y=
.
设f(t)=t+
(t∈[a2,4a2]).
若a2≤t1<t2≤2a2,则f(t1)-f(t2)=
>0
所以f(t)在[a2,2a2]上是减函数.同理可得f(t)在[2a2,4a2]上是增函数.
于是当t=2a2即x=
a时,ymin=
a,此时DE∥BC,且AD=
a.
当t=a2或t=4a2即x=a或2a时,ymax=
a,此时DE为AB或AC上的中线.
故当取AD=
a且DE∥BC时,DE最短;当D与B重合且E为AC中点,或E与C重合且D为AB中点时,DE最长.
所以xAE=
| 1 |
| 2 |
| 2a2 |
| x |
在△ADE中,由余弦定理得y=
x2+
|
因为0≤AD≤2a,0≤AE≤2a,所以
|
故y关于x的函数关系式为y=
x2+
|
(2)令t=x2,则a2≤t≤2a2,且y=
t+
|
设f(t)=t+
| 4a4 |
| t |
若a2≤t1<t2≤2a2,则f(t1)-f(t2)=
| (t1-t2)(t1t2-4a4) |
| t1t2 |
所以f(t)在[a2,2a2]上是减函数.同理可得f(t)在[2a2,4a2]上是增函数.
于是当t=2a2即x=
| 2 |
| 2 |
| 2 |
当t=a2或t=4a2即x=a或2a时,ymax=
| 3 |
故当取AD=
| 2 |

练习册系列答案
相关题目
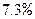 ,约多少年后我国的GDP在1999年的基础上翻两番?
,约多少年后我国的GDP在1999年的基础上翻两番?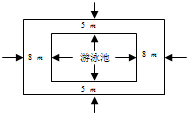

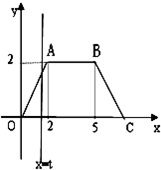
 (-x2+6x)的值域( )
(-x2+6x)的值域( )