Question

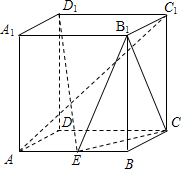如图，在直四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD为平行四边形，且AD=2，AB=AA₁=4，∠BAD=60°，E为AB的中点．
（Ⅰ） 证明：AC₁∥平面EB₁C；
（Ⅱ）求直线ED₁与平面EB₁C所成角．

Answer 1

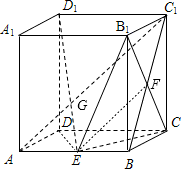解法一：（Ⅰ） 证明：连接BC₁，B₁C∩BC₁=F，连接EF，
因为AE=EB，FB=FC₁，所以EF∥AC₁（2分
因为AC₁?面EB₁C，EF?面EB₁C
所以AC₁∥面EB₁C（4分）
（Ⅱ）设AC₁与ED₁交于点G，连DE，
∵AC₁∥面EB₁C，∴G与C₁到平面EB₁C的距离相等，设为h，（6分）
则ED₁=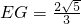，． （7分）
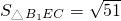∴，点E到平面B₁CC₁距离为．
又∵，
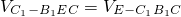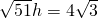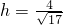∴．∴．（10分）
设ED₁与面EB₁C所成角为α，则．
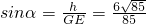所以ED₁与面EB₁C所成角为arcsin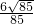． （12分）
解法二：
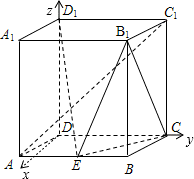
作DH⊥AB，分别令DH，DC，DD₁为x轴，y轴，z轴，如图建立坐标系┉（1分）
因为∠BAD=60°，AD=2，所以AH=1，，
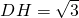所以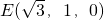D₁（0，0，4），C（0，4，0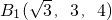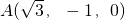），，C₁（0，4，4）（3分）
（Ⅰ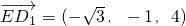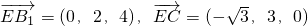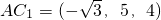），，（4分）
设面EB₁C的法向量为=（x，y，z），所以，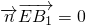
化简得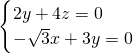令y=1，则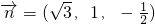．（6分）
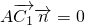∵，AC₁?面EB₁C，∴AC₁∥面EB₁C．（8分）
（Ⅱ）设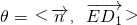，则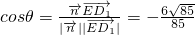．（10分）
设直线ED₁与面EB₁C所成角为α，则cosθ=cos（α+90°）=-sinα．
即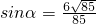．（11分）
∴直线ED₁与面EB₁C所成的角的大小为arcsin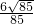． （12分）
分析：解法一：
（Ⅰ） 证明线面平行，即证AC₁平行于面EB₁C中的一条直线，即可；
（Ⅱ）设AC₁与ED₁交于点G，连DE，根据AC₁∥面EB₁C，可得G与C₁到平面EB₁C的距离相等，设为h，求出EG及h，即可求得ED₁与面EB₁C所成角；
解法二：
作DH⊥AB，分别令DH，DC，DD₁为x轴，y轴，z轴，建立坐标系，用坐标表示点
（Ⅰ）表示出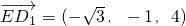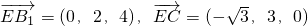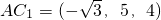，，（4分）
求出面EB₁C的法向量，证明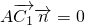，即可证得结论；
（Ⅱ）设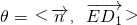，则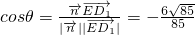，设直线ED₁与面EB₁C所成角为α，则cosθ=cos（α+90°）=-sinα，从而可求直线ED₁与面EB₁C所成的角的大小．
点评：本题考查线面平行，考查线面角，两法并举，传统方法需要添加必要的辅助线，向量方法，用代数方法解决几何问题，注意细细体会．