题目内容
函数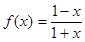 .满足
.满足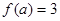 ,则
,则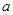 的值为( )
的值为( )
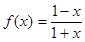 .满足
.满足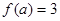 ,则
,则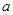 的值为( )
的值为( )A.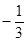 | B.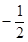 | C.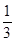 | D.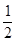 |
B
试题分析:因为,函数
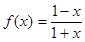 .满足
.满足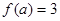 ,
,所以,
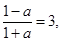 解得,
解得,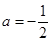 ,故选B。
,故选B。点评:简单题,利用函数的定义,建立a的方程求解。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
题目内容
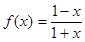 .满足
.满足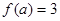 ,则
,则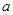 的值为( )
的值为( )A.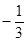 | B.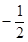 | C.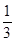 | D.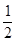 |
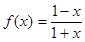 .满足
.满足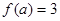 ,
,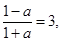 解得,
解得,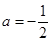 ,故选B。
,故选B。
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案