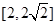题目内容
若曲线 上存在垂直y轴的切线,则实数a的取值范围是( )
上存在垂直y轴的切线,则实数a的取值范围是( )
A. | B.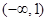 | C.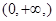 | D.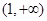 |
A
解析试题分析:由题意该函数的定义域x>0,由f′(x)=2ax+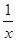 .因为存在垂直于y轴的切线,故此时斜率为0,问题转化为x>0范围内导函数f′(x)=2ax+
.因为存在垂直于y轴的切线,故此时斜率为0,问题转化为x>0范围内导函数f′(x)=2ax+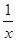 存在零点.再将之转化为g(x)=-2ax与h(x)=
存在零点.再将之转化为g(x)=-2ax与h(x)=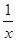 存在交点.当a=0不符合题意,当a>0时,如图1,数形结合可得显然没有交点,当a<0如图2,此时正好有一个交点,故有a<0应填(-∞,0),故答案为:{a|a<0},选A.
存在交点.当a=0不符合题意,当a>0时,如图1,数形结合可得显然没有交点,当a<0如图2,此时正好有一个交点,故有a<0应填(-∞,0),故答案为:{a|a<0},选A.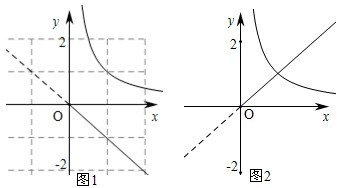
考点:1.利用导数研究曲线上某点切线方程;2.函数零点;3.数形结合思想、化归与转化思想

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设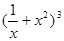 的展开式的常数项为
的展开式的常数项为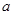 ,则直线
,则直线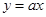 与曲线
与曲线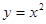 围成图形的面积为( )
围成图形的面积为( )
A.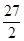 | B.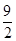 | C.9 | D. |
若函数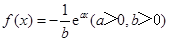 的图象在
的图象在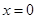 处的切线与圆
处的切线与圆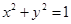 相切,则
相切,则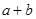 的最大值是( )
的最大值是( )
| A.4 | B.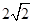 | C.2 | D.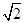 |
记函数 的最大值为M,最小值为m,则
的最大值为M,最小值为m,则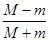 的值为( )
的值为( )
A.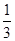 | B. | C.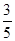 | D. |
若函数 在
在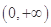 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A.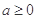 | B.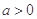 | C.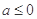 | D.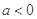 |
设函数 满足
满足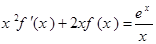 ,
, ,则当
,则当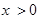 时,
时, ( )
( )
| A.有极大值,无极小值 | B.有极小值,无极大值 |
| C.既无极大值,也无极小值 | D.既有极大值,又有极小值 |
已知曲线方程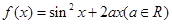 ,若对任意实数
,若对任意实数 ,直线
,直线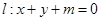 都不是曲线
都不是曲线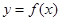 )的切线,则
)的切线,则 的取值范围是( )
的取值范围是( )
A.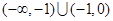 | B.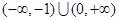 |
C.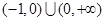 | D. 且 且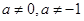 |
曲线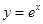 在点
在点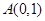 处的切线为( )
处的切线为( )
A.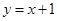 | B.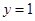 | C.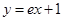 | D.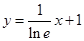 |
 上的点,且曲线C在点P处的切线的倾斜角的取值范围为
上的点,且曲线C在点P处的切线的倾斜角的取值范围为 ,则点P的横坐标的取值范围为( )
,则点P的横坐标的取值范围为( )