题目内容
求1+| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+4 |
| 1 |
| 1+2+3+…+n |
分析:由题设条件,先求出第k项ak=
=
,再由错位相减法求和.
| 1 |
| 1+2++k |
| 2 |
| k(k+1) |
解答:解:∵ak=
=
,
∴Sn=2[
+
++
]
=2[(1-
)+(
-
)++(
-
)=2(1-
)=
.
| 1 |
| 1+2++k |
| 2 |
| k(k+1) |
∴Sn=2[
| 1 |
| 1•2 |
| 1 |
| 2•3 |
| 1 |
| n(n+1) |
=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2n |
| n+1 |
点评:本题考查数列的求和,解题时要根据题设条件先求出第k项ak=
=
,再由错位相减法求和.
| 1 |
| 1+2++k |
| 2 |
| k(k+1) |

练习册系列答案
相关题目
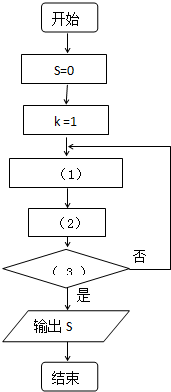 根据下面的要求,求
根据下面的要求,求 A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.