题目内容
 A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.B.运用旋转矩阵,求直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程.
C.已知A是曲线ρ=3cosθ上任意一点,求点A到直线ρcosθ=1距离的最大值和最小值.
D.证明不等式:
| 1 |
| 1 |
| 1 |
| 1×2 |
| 1 |
| 1×2×3 |
| 1 |
| 1×2×3×L×n |
分析:选A,根据切割线定理可知AD2=AE•AB,AB=4,EB=3,利用△ADE∽△ACO,可求CD的长.
选B,先写成旋转矩阵,再得出旋转前后坐标之间的关系,代入已知方程,即可得答案.
选C,两边同乘以ρ,利用公式可得直角坐标方程,进而可求点线距离的最值;
选D,将坐标的分母缩小,进而利用等比数列的求和公式,从而得证.
选B,先写成旋转矩阵,再得出旋转前后坐标之间的关系,代入已知方程,即可得答案.
选C,两边同乘以ρ,利用公式可得直角坐标方程,进而可求点线距离的最值;
选D,将坐标的分母缩小,进而利用等比数列的求和公式,从而得证.
解答:A.解:根据切割线定理可知AD2=AE•AB,
∵AD=2,AE=1
∴AB=4,EB=3,
∵AB是圆的直径
∴DE⊥DB
∵DE⊥OC
∴DE∥OC
∴△ADE∽△ACO,
∴CD=3
B.设直线2x+y-1=0上任意一点(x0,y0)旋转变换后(x0′,y0′)
∵逆时针旋转45°
∴旋转矩阵为
∴
=
∴
∴直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程是
x+
y-
x+
y-1=0
C.将极坐标方程转化成直角坐标方程:
ρ=3cosθ,两边同乘以ρ,即得:x2+y2=3x,
∴圆的方程为(x-
)2+y2=
,
又ρcosθ=1即x=1,
∴直线与圆相交
∴所求最大值为2,最小值为0.
D.证明:
+
+
+L+
<1+
+
++
=1+
=2-
<2,
从而得证.
∵AD=2,AE=1
∴AB=4,EB=3,
∵AB是圆的直径
∴DE⊥DB
∵DE⊥OC
∴DE∥OC
∴△ADE∽△ACO,
∴CD=3
B.设直线2x+y-1=0上任意一点(x0,y0)旋转变换后(x0′,y0′)
∵逆时针旋转45°
∴旋转矩阵为
|
∴
|
|
|
∴
|
∴直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程是
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
C.将极坐标方程转化成直角坐标方程:
ρ=3cosθ,两边同乘以ρ,即得:x2+y2=3x,
∴圆的方程为(x-
| 3 |
| 2 |
| 9 |
| 4 |
又ρcosθ=1即x=1,
∴直线与圆相交
∴所求最大值为2,最小值为0.
D.证明:
| 1 |
| 1 |
| 1 |
| 1×2 |
| 1 |
| 1×2×3 |
| 1 |
| 1×2×3×L×n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
=1+
| ||||
1-
|
=2-
| 1 |
| 2 n-1 |
从而得证.
点评:本题是选做题,难度相等,综合考查学生对系列4的掌握程度,综合性强.

练习册系列答案
相关题目
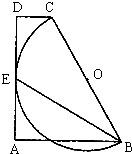 已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,垂足为A,以腰BC为直径的半圆O切AD于点E,连接BE,若BC=6,∠EBC=30°,则梯形ABCD的面积为
已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,垂足为A,以腰BC为直径的半圆O切AD于点E,连接BE,若BC=6,∠EBC=30°,则梯形ABCD的面积为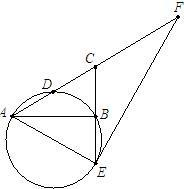 已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.
已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.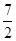 D.
D.

 +
+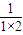 +
+ +L+
+L+ <2.
<2.