题目内容
定义在 上的偶函数
上的偶函数 满足
满足 ,且
,且 ,则
,则
的值为( )
A. | B. | C. | D. |
C
解析试题分析:根据题意可知,偶函数则满足f(-x)=f(x),那么由定义在 上的偶函数
上的偶函数 满足
满足 令
令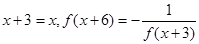 ,两式联立可知,得到
,两式联立可知,得到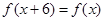 ,进而说明函数的周期性为6,那么可知2012=6
,进而说明函数的周期性为6,那么可知2012=6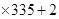 ,所以则利用周期性得到f(2012)=f(2),而f(2)=f(2-6)=f(-4),因为是偶函数,f(-4)=f(4),故可知f(2012)= f(4)=1,选C.
,所以则利用周期性得到f(2012)=f(2),而f(2)=f(2-6)=f(-4),因为是偶函数,f(-4)=f(4),故可知f(2012)= f(4)=1,选C.
考点:本试题主要考查了函数的奇偶性和周期性的运用。
点评:解决该试题的关键是能根据已知的抽象函数关系式得到函数的 周期为6.进而结合奇偶性得到函数 =f(2)=f(-4)-f(4)得到结论。
=f(2)=f(-4)-f(4)得到结论。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
函数 的值域是 ( )
的值域是 ( )
A.(- ) ) | B.(-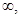 0) 0) (0,+ (0,+ ) ) |
C.(-1,+ ) ) | D.(- ,-1) ,-1) (0,+ (0,+ ) ) |
 是定义在[-6,6]上的偶函数,且
是定义在[-6,6]上的偶函数,且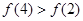 ,则下列各式一定成立的是( )
,则下列各式一定成立的是( )
A.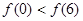 | B.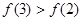 |
C.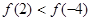 | D.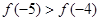 |
设偶函数 的定义域为R,当
的定义域为R,当 时
时 是增函数,则
是增函数,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( ).
| A.y=x3 | B.y=|x|+1 |
C. | D.y=2-|x| |
下列各图像中,不可能是函数 的图像的有几个( )
的图像的有几个( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下列函数中,既是偶函数又在 单调递增的是( )
单调递增的是( )
A. | B. |
C. | D. |
设奇函数 在
在 上是增函数,且
上是增函数,且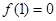 ,则不等式
,则不等式 的解集为( )
的解集为( )
A.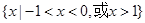 | B. |
C. | D. |
 上的函数
上的函数 满足下列条件:①对任意的
满足下列条件:①对任意的 都有
都有 ;②若
;②若 ,都有
,都有 ;③
;③ 是偶函数,则下列不等式中正确的是()
是偶函数,则下列不等式中正确的是()


