Question

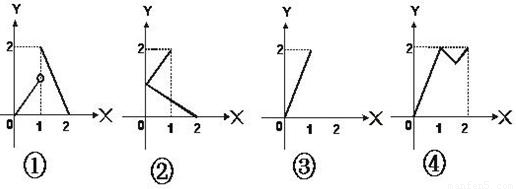
设集合P=x|0≤x≤4，Q=y|0≤y≤2，下列对应f中不能构成A到B的映射的是 ______（只填写序号）．
①y=

1

2

x ②y=

1

3

x  ③y=

2

3

x   ④y=

1

8

x．

Answer 1

①y=

1

2

x，x在集合P={x|0≤x≤4 }中任取一个值，在Q={y|0≤y≤2}中都有唯一确定的一个 y值与之对应，
故①能构成A到B的映射．
②y=

1

3

x，x在集合P={x|0≤x≤4 }中任取一个值，在Q={y|0≤y≤2}中都有唯一确定的一个 y值与之对应，
故②能构成A到B的映射．
③y=

2

3

x，对集合P={x|0≤x≤4 }中的元素4，在Q={y|0≤y≤2}中没有元素和它对应，故③不能构成A到B的映射．
④y=

1

8

x，x在集合P={x|0≤x≤4 }中任取一个值，在Q={y|0≤y≤2}中都有唯一确定的一个 y值与之对应，
故④能构成A到B的映射．
综上，①②④能构成A到B的映射，③不能，故答案选 ③．