题目内容
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() ,
,![]() .
.
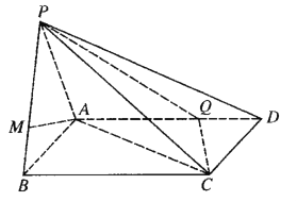
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)首先在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,根据已知条件得到
,根据已知条件得到![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,从而得到
,从而得到![]() ,四边形
,四边形![]() 是平行四边形,即
是平行四边形,即![]() ,再利用线面平行的判定即可证明.
,再利用线面平行的判定即可证明.
(2)首先取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,根据
,根据![]() ,得到
,得到![]() .利用面面垂直的性质得到
.利用面面垂直的性质得到![]() 平面
平面![]() ,从而得到
,从而得到![]() ,再利用线面垂直的性质即可证明
,再利用线面垂直的性质即可证明![]() 平面
平面![]() ,从而得到
,从而得到![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,再计算其正弦值即可.
所成的角,再计算其正弦值即可.
(1)在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,
,
如图所示: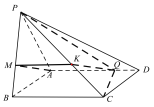
因为![]() ,所以
,所以![]() ,
,
所以![]() ,且
,且![]() .
.
又因为![]() ,所以
,所以![]() ,且
,且![]() .
.
所以![]() ,四边形
,四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,如图所示:
,如图所示:
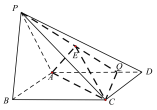
因为![]() ,则
,则![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
即![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]() ,
,
![]() .
.

练习册系列答案
相关题目