题目内容
(08年银川一中三模文)(12分) 已知椭圆C:![]() (a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,
(a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,![]() )在直线x=
)在直线x=![]() 上,且|F1F2|=|PF2|,直线
上,且|F1F2|=|PF2|,直线![]() :y=kx+m为动直线,且直线
:y=kx+m为动直线,且直线![]() 与椭圆C交于不同的两点A、B。
与椭圆C交于不同的两点A、B。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围;
的取值范围;
解析:椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() , ……2分
, ……2分
又![]() ,
,![]() ,
, ![]() ………3分
………3分
解得![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() . ………5分
. ………5分
(Ⅱ)由 ,得
,得![]() .
.
设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,则
,则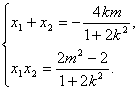 ……7分
……7分
![]() .
.
(1)当![]() 时,点
时,点![]() 、
、![]() 关于原点对称,则
关于原点对称,则![]() .
.
(2)当![]() 时,点
时,点![]() 、
、![]() 不关于原点对称,则
不关于原点对称,则![]() ,
,
由![]() ,得
,得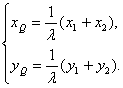 即
即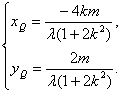
![]() 点
点![]() 在椭圆上,
在椭圆上,
![]() 有
有![]() ,
,
化简,得![]() .
.
![]() ,
,![]() 有
有![]() .………………① ……………9分
.………………① ……………9分
又![]() ,
,
![]() 由
由![]() ,得
,得![]() .……………………………② ………………10分
.……………………………② ………………10分
将①、②两式,得![]() .
.
![]() ,
,![]() ,则
,则![]() 且
且![]() .
.
综合(1)、(2)两种情况,得实数![]() 的取值范围是
的取值范围是![]() . ……………12分
. ……………12分

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
