题目内容

已知函数f（x）=e|lnx|-|x-
1
x
|，则函数y=f（x）的大致图象为（　　）
A、
B、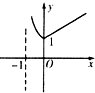
C、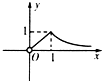
D、
考点：函数的图象
专题：函数的性质及应用
分析：利用排除法，根据定义域排除A，B，根据f（1）=1排除D，问题得以解决
解答： 解：∵f（x）=e|lnx|-|x-
1
x
|，
∴函数的定义域为（0，+∞），故排除A，B，
当x=1时，f（1）=1-0=1，故排除D
故选：C
点评：本题考查了函数图象的识别，排除法时做选择题的一种常用方法，属于基础题
练习册系列答案
相关题目
在△ABC中，a，b，c分别为三个内角A，B，C的对边，且acosB=3，bsinA=4．
（1）求边长a；
（2）若△ABC的面积S=10，求△ABC的周长．
已知集合A={x|
x-1
x+1
＜0}，B={x||x-1|＜2}，则∁BA=
 
．
在平面直角坐标系xOy中，直线y=2x+b是曲线y=alnx的切线，则当a＞0时，实数b的最小值是
 
．
定义在R上的函数满足f（x）=f（x+2），当x∈[1，3]时，f（x）=2-|x-2|，则（　　）
A、f(sin
π
6
)＜f(cos
π
6
)
B、f （sin1）＞f （cos1）
C、f(cos
2π
3
)＜f(sin
2π
3
)
D、f （cos2）＞f （sin2）
若关于x的方程
-x2-2x
=m-x有两个不等的实根，则m的取值范围是（　　）
A、（-
2
-1，
2
）
B、（-2，
2
-1）
C、（0，
2
-1）
D、[0，
2
-1）
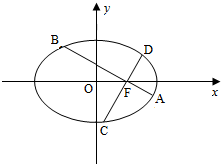如图，在平面直角坐标系xOy中，椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，过椭圆右焦点F作两条互相垂直的弦AB与CD．当直线AB斜率为0时，|AB|+|CD|=3
2
．
（Ⅰ）求椭圆的方程；
（Ⅱ）求由A，B，C，D四点构成的四边形的面积的取值范围．
已知函数f（x）=mx+3，g（x）=x2+2x+m，G（x）=f（x）-g（x）．
（1）求证：函数G（x）必有零点；
（2）若m=6，试作出函数|G（x）|的简图，并写出它的单调区间；
（3）若函数|G（x）|在[-1，0]上是减函数，求实数m的取值范围．
已知等差数列{an}中，a3+a6=17，a1a8=-38且a1＜a8．
（Ⅰ）求{an}的通项公式；
（Ⅱ）调整数列{an}的前三项a1，a2，a3的顺序，使它成为等比数列{bn}的前三项，求{bn}的通项公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网