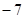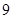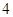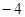题目内容
已知向量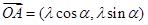
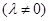 ,
,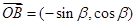 ,其中
,其中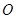 为坐标原点.
为坐标原点.
(Ⅰ)若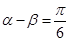 且
且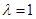 ,求向量
,求向量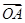 与
与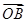 的夹角;
的夹角;
(Ⅱ)若不等式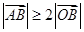 对任意实数
对任意实数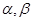 都成立,求实数
都成立,求实数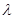 的取值范围.
的取值范围.
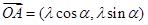
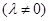 ,
,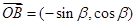 ,其中
,其中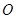 为坐标原点.
为坐标原点.(Ⅰ)若
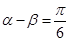 且
且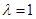 ,求向量
,求向量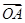 与
与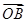 的夹角;
的夹角;(Ⅱ)若不等式
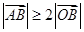 对任意实数
对任意实数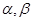 都成立,求实数
都成立,求实数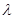 的取值范围.
的取值范围.(1)当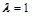 时,向量
时,向量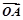 与
与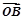 的夹角
的夹角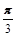 ;(2)
;(2)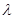 的范围是
的范围是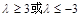 .
.
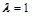 时,向量
时,向量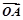 与
与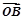 的夹角
的夹角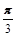 ;(2)
;(2)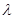 的范围是
的范围是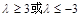 .
.(1)当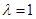 时,由向量的数量积公式即求出向量
时,由向量的数量积公式即求出向量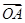 与
与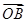 的夹角;
的夹角;
(2)不等式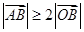 对任意实数
对任意实数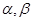 都成立, 即
都成立, 即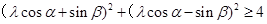 ,对任意的
,对任意的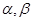 恒成立,即
恒成立,即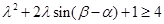 对任意的
对任意的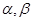 恒成立,从而转化为关于
恒成立,从而转化为关于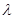 的二次不等式恒成立来解决.
的二次不等式恒成立来解决.
(1)当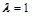 时,向量
时,向量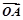 与
与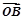 的夹角
的夹角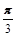 ;(6分)
;(6分)
(2)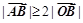 对任意的
对任意的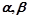 恒成立,即
恒成立,即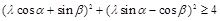
对任意的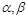 恒成立,即
恒成立,即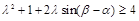 对任意的
对任意的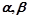 恒成立,
恒成立,
所以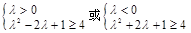 ,解得
,解得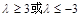 ,
,
故所求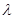 的范围是
的范围是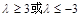 .(12分)
.(12分)
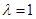 时,由向量的数量积公式即求出向量
时,由向量的数量积公式即求出向量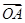 与
与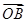 的夹角;
的夹角;(2)不等式
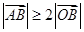 对任意实数
对任意实数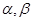 都成立, 即
都成立, 即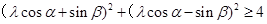 ,对任意的
,对任意的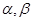 恒成立,即
恒成立,即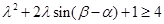 对任意的
对任意的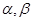 恒成立,从而转化为关于
恒成立,从而转化为关于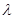 的二次不等式恒成立来解决.
的二次不等式恒成立来解决.(1)当
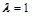 时,向量
时,向量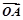 与
与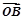 的夹角
的夹角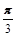 ;(6分)
;(6分)(2)
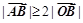 对任意的
对任意的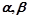 恒成立,即
恒成立,即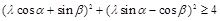
对任意的
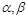 恒成立,即
恒成立,即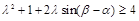 对任意的
对任意的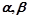 恒成立,
恒成立,所以
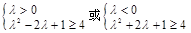 ,解得
,解得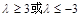 ,
,故所求
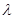 的范围是
的范围是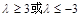 .(12分)
.(12分)
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
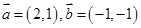 ,若
,若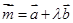 ,其中
,其中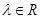 ,则
,则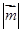 的最小值为---------------
的最小值为--------------- 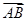 =(5,-3),C(-1,3),
=(5,-3),C(-1,3),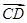 =2
=2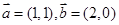 ,则向量
,则向量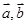 的夹角为( ).
的夹角为( ).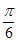
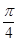
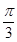
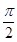
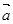 =(1,2),
=(1,2),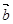 =(
=(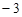 ,2),当k为何值时
,2),当k为何值时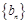 的前
的前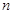 项和为
项和为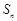 ,
,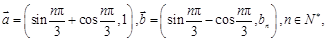 且
且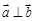
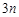 项的和.
项的和. 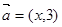 (
(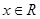 ),则“
),则“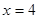 ”是“
”是“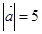 ”的( )
”的( )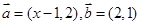 ,则
,则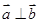 的充要条件是 ( )
的充要条件是 ( )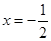
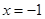
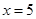
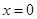
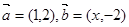 ,且
,且 ,则实数
,则实数 等于( )
等于( )